Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
One does not simply tell the odd integers to piss off.I was thinking about that before actually. Maybe just tell the odd integers to piss off?
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
One does not simply tell the odd integers to piss off.I was thinking about that before actually. Maybe just tell the odd integers to piss off?
Yeah when I was doing that question I got up to the n/2 step but I didnt want to continue because I thought it was mathematically incorrect to assume n was even lol. So I ended up not doing it :/One does not simply tell the odd integers to piss off.
roflOne does not simply tell the odd integers to piss off.
lol'd at this. One thing carrot, just make sure BoardOS doesn't get hold of your paper.I was thinking about that before actually. Maybe just tell the odd integers to piss off?
Yeah got the same except for Q1 which I got D (which has already been pointed out)My multiple choice answers:
1. B
2. C
3. D
4. A
5. C
6. B
7. D
8. D
9. B
10. D
anyone the same or different?
Did anyone get the last perms question? part biii of Q11
Yeah you can do it without cases and its pretty easy though I think I got it wrong because I forgot about the H'sI have a feeling carrot may have underestimated its difficulty. If there was no double H's it would have been fine... but maybe there is an easy way
Haha lol. You should so do this in HSCI was thinking about that before actually. Maybe just tell the odd integers to piss off?
Here's something to start you off:

he came, he considered, he did not conquer. nvm ill have a good think laterAnother hint, consider
and
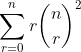
oh yes ofc! well done
Oh lol got it.I still cant to that perms one lol, can someone post their solution up
Could you explain how you got 8 spots left for vowels?Oh lol got it.
Taking the 7 consonants, there are 7!/2 ways to arrange. Now there are 8 spots for vowels and they can be put in in 8P4/3! ways. I think that's right...
Ok this is called the insertion method- I won't give the answer but I'll tell you how to do it and you should be able to do the rest. So we don't want any two vowels next to each other. If we set up the other letters as like 'barriers' then by placing one vowel between the barriers (i.e. not two between the same barrier), then by definition all vowels are seperated as required. Now we have 7 other letters so there are seven barriers and hence 8 spaces for the vowels to go (draw this out if you can't picture it). Now we just need to place the 4 vowels in these 8 different spots so just use your normal combinatorics (accounting for the triple O etc.) and then you rearrange the arrangements of the 'barriers' and you're done.Could you explain how you got 8 spots left for vowels?
My my... this method looks familiar =pOk this is called the insertion method- I won't give the answer but I'll tell you how to do it and you should be able to do the rest. So we don't want any two vowels next to each other. If we set up the other letters as like 'barriers' then by placing one vowel between the barriers (i.e. not two between the same barrier), then by definition all vowels are seperated as required. Now we have 7 other letters so there are seven barriers and hence 8 spaces for the vowels to go (draw this out if you can't picture it). Now we just need to place the 4 vowels in these 8 different spots so just use your normal combinatorics (accounting for the triple O etc.) and then you rearrange the arrangements of the 'barriers' and you're done.
Does that make sense?
Haha yes I have to give acknowledgements- Carrot taught me this. I think I still got the question wrong though because I think I forgot about the H'sMy my... this method looks familiar =p
Ah that is genius heh. Well this method will probably help me with alot of perms questions. Thanks (and props to carrot of course)Ok this is called the insertion method- I won't give the answer but I'll tell you how to do it and you should be able to do the rest. So we don't want any two vowels next to each other. If we set up the other letters as like 'barriers' then by placing one vowel between the barriers (i.e. not two between the same barrier), then by definition all vowels are seperated as required. Now we have 7 other letters so there are seven barriers and hence 8 spaces for the vowels to go (draw this out if you can't picture it). Now we just need to place the 4 vowels in these 8 different spots so just use your normal combinatorics (accounting for the triple O etc.) and then you rearrange the arrangements of the 'barriers' and you're done.
Does that make sense?

