Binomial Theorem,
I will leave Blaise Pascal's Triangle here.
First let's define a special property.
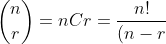!r!})
(You will be seeing this alot.)
Secondly,
We need to define the expansion of
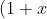^n=nC0 +nC1x+nC2x^2+nC3x^3....nCnx^n)
(I am sure you know this already, I am just doing it as a refresher.
In similar style,
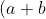^n=nC0x^n + nC1x^n^-^1y+nC2+x^n^-^2y^2+nC3+x^n^-^3y^3....+nCny^n)
(Noting that the first term decreasing by a degree of 1 each time and the second term increases by a degree of 1.)
Let us so a few questions on this. No biggy.
Expand:
Q1.
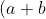^4=4C0(a^4)+4C1 (a^3)b +4C2 (a^2)b^2+4C3 a b^3 +4C4(b^4))
(Why did I write the coefficients? To help you understand where it is coming from. It's coming from our pascal's triangle.
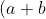^4=(a^4)+4(a^3)b +6(a^2)b^2+4 a b^3 +1(b^4))
^4=a^4+4a^3b +6a^2b^2+4a b^3 +b^4)
Q2.
^3=3C0x^3 + 3C1x^2 (-\frac{1}{x}) + 3C2x(-\frac{1}{x})^2 + 3C3(-\frac{1}{x})^3)
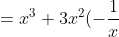 + 3x(-\frac{1}{x})^2 + 1(-\frac{1}{x})^3)
^3=x^3-3x+\frac{3}{x}-\frac{1}{x^3})
Now, this is baby maths. Let's get onto the interesting stuff.
Expand the term
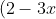^5)
as far as
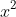
. The find the term in
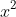
in the expansion
(2-3x)^5)
We obviously have no choice, we will expand this quickly,
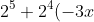+2^3(-3x)^2....)
(We don't need to continue, we see
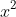
already and by inspection, we can see if we continue, no other terms will produce
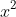
.)
Let's do this!
+2^3(-3x)^2....)(x+7))
By using your eyes, we can see that the following make babies with
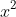
,
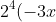*x+2^3(-3x)^2*7)
(The rest we abandon.)

Hence the term in
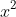
in the expansion is,

General term:
Love (Relationships of Bionomial Coefficients.
Let's look at some past questions.
Equating coefficients (1st type.)
Example 1: 2010 3U HSC

This question is very simple. It requires you to recognise that,

Let's just now focus on the first part:
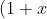^n=\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3....+\binom{n}{n}x^n)
If we let
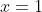

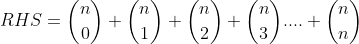
(No more

!)

Hence
 Example 2:
Example 2: From tutoring.
^n\: \textup{and}\: (1-x)^n \textup{and by choosing appropriate values for }x \:\textup{and}\: n \textup{prove that:})
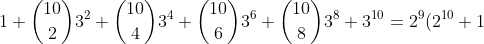)
Obviously, we need to consider two expansions:
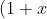^n=\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n)
(1)
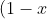^n=\binom{n}{0}-\binom{n}{1}x+\binom{n}{2}x^2-\binom{n}{3}x^3-....+\binom{n}{n}x^n)
(2) (Note, the sign alternates. That is a BIG clue!)
Let's select some nice numbers,
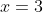
(Since we know that the coefficients are in front of 3s!)
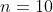
(We know that the RHS has something to do with 10s.)
From (1),
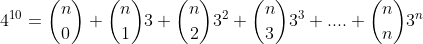
(1)[/tex]
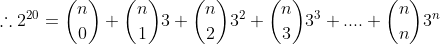
(1)[/tex]
From (2),
^1^0=\binom{n}{0}-\binom{n}{1}(-3)+\binom{n}{2}(-3)^2+\binom{n}{3}(-3)^3+....+\binom{n}{n}(-3)^n)
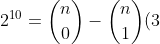+\binom{n}{2}(3)^2-\binom{n}{3}(3)^3-....+\binom{n}{n}(-3)^n)
Now, (1)+(2)
The magic happens here!

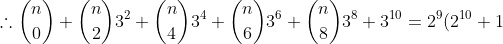)
(As required.)
Differentiating (2nd type)
Example 3: Cambridge Ex 5F. (Altered slightly by me.)
Considering:
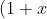^n=\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n)
Show that

Firstly, we of course as instructed, need to consider,
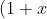^n=\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n)
We notice that there are multiples in front of each term. This is a clue to introduce calculus. Differentiation.
Taking the derivative of both sides,
^n^-^1=\binom{n}{1}+\binom2{n}{2}x+3\binom{n}{3}x^2+....+n\binom{n}{n}x^n^-^1)
We are very close to getting what we want, but pesky

is in the way. How do we get rid of an

instantly?
Let
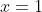
^n^-^1=\binom{n}{1}+\binom2{n}{2}(1)+3\binom{n}{3}(1)^2+....+n\binom{n}{n}(1)^n^-^1)
 Still in the process of typing and editing errors still, so stayed tuned.
Integrating
Still in the process of typing and editing errors still, so stayed tuned.
Integrating (3rd type.)
Example 4: Fitzpatrick 29 (a)
Show that,
}{n+1})
Spiral tip - Fractions indicate calculus is involved. This case, we get the value
^n=\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n)
I will integrate over the values 0, 1. Watch what happens.
^n\: {\mathrm{d} x}=\int_{0}^{1} (\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n)\: {\mathrm{d} x})
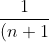}(1+x)^n^+^1=(\binom{n}{0}x+\frac{1}{2}\binom{n}{1}x^2+\frac{1}{3}\binom{n}{2}x^3+...+\frac{1}{(n+1)}\binom{n}{n}x^n^+^1))
(All with limits 0 to 1.)
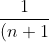}(1+1)^n^+^1-\frac{1}{(n+1)}(1+0)^n^+^1=(\binom{n}{0}(1)+\frac{1}{2}\binom{n}{1}(1)^2+\frac{1}{3}\binom{n}{2}(1)^3+...+\frac{1}{(n+1)}\binom{n}{n}(1)^n^+^1-0))
}{n+1}) Shifting by multiplication of a variable.
Shifting by multiplication of a variable.
St George 2005 3U Trial

You are in luck. This question guides you. But normally the clue to multiple by the variable x is when.
Quickly do the first couple of questions since I probably won't need to guide you through them.
a)
i. Product rule of course!
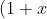^n +nx(1+x)^n^-^1)
ii)
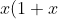^n=x[\binom{n}{0}+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+....+\binom{n}{n}x^n])
(Notice how the bottom number of the nice brackets corresponds with the degree of the polynomial. But we see when we expand it, it will shift like so...)
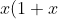^n=\binom{n}{0}x+\binom{n}{1}x^2+\binom{n}{2}x^3+\binom{n}{3}x^4+....+\binom{n}{n}x^n^+^1)
Let us now differentiate the expression.
Going to take an hour nap, then be back with more examples. Note I skipped the others, because I thought relationships are the most interesting.




