Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Australian Maths Competition (2 Viewers)
- Thread starter maths94
- Start date
Re: Australian Maths Competition 2013
Could you please show how to get it?Thanks for 28 and 29, I assume the answers are 495 and 506 respectively?
Re: Australian Maths Competition 2013
For Q28, a sum of 9 consecutive positive integers is always a multiple of 9 (it's 9 times the middle number).
Similarly a sum of 11 consecutive positive integers is always a multiple of 11.
For even numbers (when there's no middle number), it works slightly differently.
Try some and you'll see that the sum of 10 consecutive positive integers is always 5 more than a multiple of 10.
The question then comes down to a Chinese Remainder Theorem calculation.
You want a number which is a multiple of both 9 and 11, hence a multiple of 99, since 9 and 11 are coprime.
It then has to be the smallest multiple of 99 which is also 5 more than a multiple of 10.
I agree with both Q28: 495 and Q29: 506.Could you please show how to get it?
For Q28, a sum of 9 consecutive positive integers is always a multiple of 9 (it's 9 times the middle number).
Similarly a sum of 11 consecutive positive integers is always a multiple of 11.
For even numbers (when there's no middle number), it works slightly differently.
Try some and you'll see that the sum of 10 consecutive positive integers is always 5 more than a multiple of 10.
The question then comes down to a Chinese Remainder Theorem calculation.
You want a number which is a multiple of both 9 and 11, hence a multiple of 99, since 9 and 11 are coprime.
It then has to be the smallest multiple of 99 which is also 5 more than a multiple of 10.
Re: Australian Maths Competition 2013

A slight miscalculation I think... make that 161 for Q27For 26, 27 and 30 I get 512, 162 and 765 respectively
Re: Australian Maths Competition 2013
Here's another variation: Since the line divides the shaded area in half (this is only true because it also divides the whole rectangle in half, by the way), it must past through the midpoint of the line connecting the circles' centres. If we take P as (0,0) and C as (6,2), this midpoint is (2.5, 1). Then the gradient and y-intercept of the line can easily be shown to be both 2/7, pretty much as you did before.
Another way to get this gradient is to imagine 'sliding' the right hand circle up the line like a bead along a wire, to sit in the top right hand corner of the rectangle, with new centre (11,3) - this gives the same sort of nice symmetrical picture you used to choose XP = 1.
Looks good.Hope this actually makes sense, solution to question 22:

Here's another variation: Since the line divides the shaded area in half (this is only true because it also divides the whole rectangle in half, by the way), it must past through the midpoint of the line connecting the circles' centres. If we take P as (0,0) and C as (6,2), this midpoint is (2.5, 1). Then the gradient and y-intercept of the line can easily be shown to be both 2/7, pretty much as you did before.
Another way to get this gradient is to imagine 'sliding' the right hand circle up the line like a bead along a wire, to sit in the top right hand corner of the rectangle, with new centre (11,3) - this gives the same sort of nice symmetrical picture you used to choose XP = 1.
RealiseNothing
what is that?It is Cowpea
Re: Australian Maths Competition 2013
Very nice alternative methods as well.
Yep, I know the bolded.Looks good.
Here's another variation: Since the line divides the shaded area in half (this is only true because it also divides the whole rectangle in half, by the way), it must past through the midpoint of the line connecting the circles' centres. If we take P as (0,0) and C as (6,2), this midpoint is (2.5, 1). Then the gradient and y-intercept of the line can easily be shown to be both 2/7, pretty much as you did before.
Another way to get this gradient is to imagine 'sliding' the right hand circle up the line like a bead along a wire, to sit in the top right hand corner of the rectangle, with new centre (11,3) - this gives the same sort of nice symmetrical picture you used to choose XP = 1.
Very nice alternative methods as well.
Re: Australian Maths Competition 2013

If you're doing something like the Melb Uni maths comp where you need to write out reasoning as well as the answer, you can use induction to rigorously prove various statements, e.g.:
there are 2 x (3^n) ways of the first 2n+1 goals being scored (at which time one team or the other will be 1 goal ahead)
or (what we really need here):
there are 4 x (3^n) ways of the first 2n+2 goals being scored.
You have the pattern and the reasoning already, all of this just serves to formalise it a bit more so you can be sure that the pattern does continue & you are correct
972 is correct, and a nice way to picture things is with a trellis showing possible scores and the numbers of ways of reaching them. Apologies for the crappy image, but since you already have the working I think you can get the picture - the numbers are added like in Pascal's triangle:Consider the scores are equal at (x,x), then you have two possibilities (x+1,x) or (x,x+1).
If the scores are unequal at (x,x+1) you also have two possibilities (x+1,x+1) or (x,x+2).
However if the scores are 2 apart (x,x+2) you only have one possibility (x+1,x+2).
Start at (0,0) and apply this, you find the pattern is double then add half of what you have, i.e.:
1) 2
2) 4
3) 6
4) 12
5) 18
6) 36
7) 54
8) 108
9) 162
10) 324
11) 486
12) 972
I might add I don't know for sure if my answers are correct, I'm just posting my personal working out.

If you're doing something like the Melb Uni maths comp where you need to write out reasoning as well as the answer, you can use induction to rigorously prove various statements, e.g.:
there are 2 x (3^n) ways of the first 2n+1 goals being scored (at which time one team or the other will be 1 goal ahead)
or (what we really need here):
there are 4 x (3^n) ways of the first 2n+2 goals being scored.
You have the pattern and the reasoning already, all of this just serves to formalise it a bit more so you can be sure that the pattern does continue & you are correct
x3reme_c00l
New Member
- Joined
- Jul 26, 2011
- Messages
- 1
- Gender
- Male
- HSC
- 2008
Re: Australian Maths Competition 2013

Whenever an odd number of goals have been scored, the teams must be one goal apart.
If team X leads team Y in such a situation, the next 2 goals can be scored in 3 ways: XY, YX, YY
The teams are then one goal apart again.
So there are 2 ways the first goal can be scored, 3 ways each subsequent pair of goals can be scored, and 2 ways the final goal can be scored.
In the case of this Q, i.e. a 12-goal game, we have 2 x 3^5 x 2, in general 2 x 3^(n/2 - 1) x 2 for a game with n goals (n even) or just 2 x 3^((n-1)/2) if n is odd
I've just hit on the short and neat way of doing this QConsider the scores are equal at (x,x), then you have two possibilities (x+1,x) or (x,x+1).
If the scores are unequal at (x,x+1) you also have two possibilities (x+1,x+1) or (x,x+2).
However if the scores are 2 apart (x,x+2) you only have one possibility (x+1,x+2).
Start at (0,0) and apply this, you find the pattern is double then add half of what you have, i.e.:
1) 2
2) 4
3) 6
4) 12
5) 18
6) 36
7) 54
8) 108
9) 162
10) 324
11) 486
12) 972
I might add I don't know for sure if my answers are correct, I'm just posting my personal working out.
Whenever an odd number of goals have been scored, the teams must be one goal apart.
If team X leads team Y in such a situation, the next 2 goals can be scored in 3 ways: XY, YX, YY
The teams are then one goal apart again.
So there are 2 ways the first goal can be scored, 3 ways each subsequent pair of goals can be scored, and 2 ways the final goal can be scored.
In the case of this Q, i.e. a 12-goal game, we have 2 x 3^5 x 2, in general 2 x 3^(n/2 - 1) x 2 for a game with n goals (n even) or just 2 x 3^((n-1)/2) if n is odd
HSC2014
Member
- Joined
- Jul 30, 2012
- Messages
- 398
- Gender
- Male
- HSC
- N/A
Re: Australian Maths Competition 2013
It's the holidays so hopefully I'll receive it early next term O:So the results are out, how did you guys do?
Makematics
Well-Known Member
Re: Australian Maths Competition 2013
sooo is there any way to view amc results online? i know what award i got, but id like to see what my score was
sooo is there any way to view amc results online? i know what award i got, but id like to see what my score was
obliviousninja
(╯°□°)╯━︵ ┻━┻ - - - -
Re: Australian Maths Competition 2013
My teacher didn't bother to let us do AMC this year, she wanted to focus on hsc revision.
I think I got a distinction last year though.
Did you get the D?sooo is there any way to view amc results online? i know what award i got, but id like to see what my score was
My teacher didn't bother to let us do AMC this year, she wanted to focus on hsc revision.
I think I got a distinction last year though.
Re: Australian Maths Competition 2013
I agree that there are 7 ways of writing 2013 as the sum of at least 2 consecutive positive integers, but there certainly aren't 11 ways of writing 72 as such a sum.
Also, your formula would say that any product of 2 primes could be written as such a sum in 3 ways.
But (for example) 6 can only be written as 1+2+3, and 15 can only be written as 7+8 or 4+5+6.
Your formula appears to be the right one if you want to count how many factors a number has, other than itself... but that's not what this questiom was about ;-)
The way I've done it (just now, better late than never lol) is based on these 2 observations:
- if n is odd, the sum of any n consecutive integers is a multiple of n
- if n is even, the sum of any n consecutive integers is n/2 more than a multiple of n
I think you've got the right answer for the wrong reason here...Prime factors of 2013 are 3, 11, 61.
They all have powers of 1, thus the amount of consecutive integers that add to 2013 is:
Take another example, say 72, it's prime factorisation is
So we take each power, add one, multiply them together, and minus one:
(3+1)-1 = 11)
I agree that there are 7 ways of writing 2013 as the sum of at least 2 consecutive positive integers, but there certainly aren't 11 ways of writing 72 as such a sum.
Also, your formula would say that any product of 2 primes could be written as such a sum in 3 ways.
But (for example) 6 can only be written as 1+2+3, and 15 can only be written as 7+8 or 4+5+6.
Your formula appears to be the right one if you want to count how many factors a number has, other than itself... but that's not what this questiom was about ;-)
The way I've done it (just now, better late than never lol) is based on these 2 observations:
- if n is odd, the sum of any n consecutive integers is a multiple of n
- if n is even, the sum of any n consecutive integers is n/2 more than a multiple of n
Re: Australian Maths Competition 2013

For Q21, I started by writing x^5 = (x^2)^2 * x = (x+3)^2 * x = ..., maybe this gets to the answer a bit quicker??
I agree almost verbatim with what you did for Q23My solutions to question 21 and 23:
Question: If, what is the value of
?
Multiply each side by
Now multiply each side by
Substitute this in gives:
If you repeat this a few times you get the answer of
Question 23:
Question: Givenfind
Square both sides:
Cancel out theon each side:
Squaring again gives:
We want to find the value of, but if we make this one fraction we get:
Butso
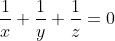
For Q21, I started by writing x^5 = (x^2)^2 * x = (x+3)^2 * x = ..., maybe this gets to the answer a bit quicker??
RealiseNothing
what is that?It is Cowpea
Re: Australian Maths Competition 2013
http://en.wikipedia.org/wiki/Polite_numberI think you've got the right answer for the wrong reason here...
I agree that there are 7 ways of writing 2013 as the sum of at least 2 consecutive positive integers, but there certainly aren't 11 ways of writing 72 as such a sum.
Also, your formula would say that any product of 2 primes could be written as such a sum in 3 ways.
But (for example) 6 can only be written as 1+2+3, and 15 can only be written as 7+8 or 4+5+6.
Your formula appears to be the right one if you want to count how many factors a number has, other than itself... but that's not what this questiom was about ;-)
The way I've done it (just now, better late than never lol) is based on these 2 observations:
- if n is odd, the sum of any n consecutive integers is a multiple of n
- if n is even, the sum of any n consecutive integers is n/2 more than a multiple of n
Re: Australian Maths Competition 2013
Thanks for the very informative link... most importantly it defines:
"the politeness of x equals the number of odd divisors of x that are greater than one" (emphasis added)
So your answer to the original problem is right for the right reason (or at least one right reason, I did it a bit differently, and more clumsily without the concept of polite numbers )
)
But because of the restriction to odd divisors, your example with 72 needs revision down to just (3+1)-1 = 2, which seems right according to my calculations: 72 = 23+24+25 (3 #s with ave 24) = 4+5+6+...+12 (9 #s with ave 8)
oops, I missed 15 = 1+2+3+4+5
Thanks for the very informative link... most importantly it defines:
"the politeness of x equals the number of odd divisors of x that are greater than one" (emphasis added)
So your answer to the original problem is right for the right reason (or at least one right reason, I did it a bit differently, and more clumsily without the concept of polite numbers
But because of the restriction to odd divisors, your example with 72 needs revision down to just (3+1)-1 = 2, which seems right according to my calculations: 72 = 23+24+25 (3 #s with ave 24) = 4+5+6+...+12 (9 #s with ave 8)
RealiseNothing
what is that?It is Cowpea
Re: Australian Maths Competition 2013
Also for the example of 72, would it not just be (3)-1= 2? Since (3+1)-1 = 3 not 2
Ah, yes that is true. I completely skimmed over the "odd" unfortunately haha.oops, I missed 15 = 1+2+3+4+5
Thanks for the very informative link... most importantly it defines:
"the politeness of x equals the number of odd divisors of x that are greater than one" (emphasis added)
So your answer to the original problem is right for the right reason (or at least one right reason, I did it a bit differently, and more clumsily without the concept of polite numbers)
But because of the restriction to odd divisors, your example with 72 needs revision down to just (3+1)-1 = 2, which seems right according to my calculations: 72 = 23+24+25 (3 #s with ave 24) = 4+5+6+...+12 (9 #s with ave 8)
Also for the example of 72, would it not just be (3)-1= 2? Since (3+1)-1 = 3 not 2
Re: Australian Maths Competition 2013
Sometimes my brain goes to sleep recently... must be because the end of the year is coming
Yes indeed, I think I was reading the wrong half of your factorisation and 72 and copied it without thinking, I meant to write the (2+1)-1 part and leave out the (3+1) coming from 2^3Ah, yes that is true. I completely skimmed over the "odd" unfortunately haha.
Also for the example of 72, would it not just be (3)-1= 2? Since (3+1)-1 = 3 not 2
Sometimes my brain goes to sleep recently... must be because the end of the year is coming


