Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Another Complex Number Question... (1 Viewer)
- Thread starter ella-m
- Start date
ohexploitable
hey
Bored Of Fail 2
Banned
- Joined
- Jan 13, 2011
- Messages
- 354
- Gender
- Male
- HSC
- N/A
finding th modulus for 35 is fairly standard, just mod = sqrt ( (real part)^2 + (imag part)^2 )
= sqrt ( ( 1+cosx)^2 + (sin(x))^2 ) = sqrt ( 2 +2cosx )
then using double angle results cosx = 2 (cos(x/2) )^2 -1 , then sub in and mod is done
argument is a fair bit harder
= sqrt ( ( 1+cosx)^2 + (sin(x))^2 ) = sqrt ( 2 +2cosx )
then using double angle results cosx = 2 (cos(x/2) )^2 -1 , then sub in and mod is done
argument is a fair bit harder
ohexploitable
hey
ohexploitable
hey
ohexploitable
hey
Bored Of Fail 2
Banned
- Joined
- Jan 13, 2011
- Messages
- 354
- Gender
- Male
- HSC
- N/A
when you go from sin (x/2) / cos ( x/2) = sqrt ( (1-cosx)/ ( 1+cosx) ) I think I kinda know what did , but im thinking there is 90% chance that the person that asked the question has no idea what you did lol
Also, I must say I am very impressed someone doing gen maths could do these questions
Also, I must say I am very impressed someone doing gen maths could do these questions
ohexploitable
hey
Bored Of Fail 2
Banned
- Joined
- Jan 13, 2011
- Messages
- 354
- Gender
- Male
- HSC
- N/A
ahh I gotcha, and the third part to that questions is relatvely easy,
just a fairly standard binomial question where you take n=4
ie consider ( 1 + ( cosx+ i sinx ) ) ^4 and then expand it using binomial theorm and use the theorm ( cos(x) + isin(x) ) ^n = cos(nx) + i sin(nx)
then equate real and imaginary parts
etc
etc
but most 4unit students wouldnt have seen that yet, most school leave binomial theorm as the last chapter of 3unit math
just a fairly standard binomial question where you take n=4
ie consider ( 1 + ( cosx+ i sinx ) ) ^4 and then expand it using binomial theorm and use the theorm ( cos(x) + isin(x) ) ^n = cos(nx) + i sin(nx)
then equate real and imaginary parts
etc
etc
but most 4unit students wouldnt have seen that yet, most school leave binomial theorm as the last chapter of 3unit math
but can you also do 34 part ii?
Bored Of Fail 2
Banned
- Joined
- Jan 13, 2011
- Messages
- 354
- Gender
- Male
- HSC
- N/A
following from that.but can you also do 34 part ii?
now it tells us that this is a real number/expression ( it says z + 1/z = k, where k is real )
so that means its imaginary part must be zero
therefore y ( x^2 +y^2 -1) / ( x^2 + y^2 ) =0
and setting each factor equal to zero gives
y=0 , or x^2 +y^2 =1
im so cluesless on the other part :|, been try to sub in the values and shit and still cnt get anywhere
Last edited:
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Suppose y=0, then z+1/z=x+1/x=k
so |k|=|x+1/x|=|(x^2+1)/x|
we use the basic inequality of x^2+1>=2x (Based on (x-1)^2>=0)
Then |k| = |(x^2+1)/x| >= |(2x)/x|=2 so |k|>=2
Suppose x^2+y^2=1:
Then |x|<=1 (as x and y are real numbers)
so subbing (x^2+y^2=1) into the equation for k will give us:
k= x(1+1)/1= 2x
Since |x|<=1, then |k|= |2x|=2|x|<=2*1=2 so |k|<=2
so |k|=|x+1/x|=|(x^2+1)/x|
we use the basic inequality of x^2+1>=2x (Based on (x-1)^2>=0)
Then |k| = |(x^2+1)/x| >= |(2x)/x|=2 so |k|>=2
Suppose x^2+y^2=1:
Then |x|<=1 (as x and y are real numbers)
so subbing (x^2+y^2=1) into the equation for k will give us:
k= x(1+1)/1= 2x
Since |x|<=1, then |k|= |2x|=2|x|<=2*1=2 so |k|<=2
ohexploitable
hey
I gave your post some protectionSuppose y=0, then z+1/z=x+1/x=k
so |k|=|x+1/x|=|(x^2+1)/x|
we use the basic inequality of x^2+1>=2x (Based on (x-1)^2>=0)
Then |k| = |(x^2+1)/x| >= |(2x)/x|=2 so |k|>=2
Suppose x^2+y^2=1:
Then |x|<=1 (as x and y are real numbers)
so subbing (x^2+y^2=1) into the equation for k will give us:
k= x(1+1)/1= 2x
Since |x|<=1, then |k|= |2x|=2|x|<=2*1=2 so |k|<=2

-----
-----
I gave your post some protection

-----
-----
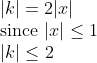
Rofls ! thanks for your help... and the protection



