What is the point of this working? can you not just use the quadratic formula?? (2 Viewers)

[v.tex]

 

[v.tex]

Has any one come across questions in formal assessments where they ask u to use this method?? i find it really confusing

 

[liamkk112]

View attachment 46348

if you use the quadratic formula you have to calculate the square root of 4-4i (or 1-i). it's basically the exact same thing

 

[v.tex]

if you use the quadratic formula you have to calculate the square root of 4-4i (or 1-i). it's basically the exact same thing

Ok but if i find quadratic formula simpler in my mind and in terms of working out would it be fine if i just use it. Or should i try and master completing the square method aswell.

 

[liamkk112]

Ok but if i find quadratic formula simpler in my mind and in terms of working out would it be fine if i just use it. Or should i try and master completing the square method aswell.

usually they don't care, they'll just ask you to find the roots of the polynomial. completing the square is basically the same thing, the only extra step is adding the term on both sides of the equation

 

[pl4smaa21]

Ok but if i find quadratic formula simpler in my mind and in terms of working out would it be fine if i just use it. Or should i try and master completing the square method aswell.

I'm not too sure on this but I think I may know why they kinda structured the course in a way that they refrain from just applying the quadratic formula every time for quadratic equations. It's because in az^2+bz+c=0, whenever a,b and c are real then it'd always be the case that the discriminant = b^2 -4ac. Will always be a real number so in the quadratic formula:

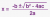
we'd always be able to compute the principal square root at the numerator and then consider the two solutions by adding and subtracting it to -b. If the discriminant = 4 then we know that sqrt(4)=2 so we'd always have a single number to place ahead of the -+ sign (note that principal sqrt is only positive entry). Similarly if we had -9=discriminant we can just as easily write it out as sqrt(9) * sqrt(i) = 3i so we'd have x=-b-+3i/2a. Notice how with the principal square root we always have ONE number we can place into the whole sqrt(discriminant) but this consistency breaks down when we get into complex territory. More specifically if a,b and c are all complex then it will often occur that the discriminant = b^2-4ac may be itself ALSO complex. But this gives rise to a problem suppose our discriminant was 7+24i . Then we'd end up with in our quadratic formula: x= -b-+sqrt(7+24i)/2a. However, the square root of 7+24i doesn't HAVE a positive and negative counterpart because positive and negative square roots don't really exist for complex numbers. The square roots of 7+24i = 4+3i and -4-3i and it isn't very rigorously defined at this point what the terms 'positive' and 'negative' really mean as they pertain to complex numbers. We can say confidently for real numbers that x is negative iff x/abs(x) = -1 and x is positive iff x/abs(x)=1 but there is no such statement (as far as I know) that you can make to class positive and negative complex numbers. So the problem is an indecision in whether to place 4+3i or -4-3i into the place of sqrt(b^2-4ac). However, in practice you can literally just choose one of the square roots sub it in for sqrt(discriminant) and get the same answers lmao. But I guess the main reason they refrain from using this method is the undefined nature of the positive square root of a complex number in the event the discriminant is complex.

P.S. I'd imagine there probably is some way to define the positive square root of a complex number as in there may be some convention but this reasoning is the one provided by the cambridge textbook below:


edit: idk if my defn of pos. and neg. numbers is RIGOROUS I just made it up cuz it felt accurate enough

 

[liamkk112]

I'm not too sure on this but I think I may know why they kinda structured the course in a way that they refrain from just applying the quadratic formula every time for quadratic equations. It's because in az^2+bz+c=0, whenever a,b and c are real then it'd always be the case that the discriminant = b^2 -4ac. Will always be a real number so in the quadratic formula:
View attachment 46378
we'd always be able to compute the principal square root at the numerator and then consider the two solutions by adding and subtracting it to -b. If the discriminant = 4 then we know that sqrt(4)=2 so we'd always have a single number to place ahead of the -+ sign (note that principal sqrt is only positive entry). Similarly if we had -9=discriminant we can just as easily write it out as sqrt(9) * sqrt(i) = 3i so we'd have x=-b-+3i/2a. Notice how with the principal square root we always have ONE number we can place into the whole sqrt(discriminant) but this consistency breaks down when we get into complex territory. More specifically if a,b and c are all complex then it will often occur that the discriminant = b^2-4ac may be itself ALSO complex. But this gives rise to a problem suppose our discriminant was 7+24i . Then we'd end up with in our quadratic formula: x= -b-+sqrt(7+24i)/2a. However, the square root of 7+24i doesn't HAVE a positive and negative counterpart because positive and negative square roots don't really exist for complex numbers. The square roots of 7+24i = 4+3i and -4-3i and it isn't very rigorously defined at this point what the terms 'positive' and 'negative' really mean as they pertain to complex numbers. We can say confidently for real numbers that x is negative iff x/abs(x) = -1 and x is positive iff x/abs(x)=1 but there is no such statement (as far as I know) that you can make to class positive and negative complex numbers. So the problem is an indecision in whether to place 4+3i or -4-3i into the place of sqrt(b^2-4ac). However, in practice you can literally just choose one of the square roots sub it in for sqrt(discriminant) and get the same answers lmao. But I guess the main reason they refrain from using this method is the undefined nature of the positive square root of a complex number in the event the discriminant is complex.

P.S. I'd imagine there probably is some way to define the positive square root of a complex number as in there may be some convention but this reasoning is the one provided by the cambridge textbook below:
View attachment 46379

edit: idk if my defn of pos. and neg. numbers is RIGOROUS I just made it up cuz it felt accurate enough

u can just say a real number x is negative if x<0 lol. but you're right, you cannot order the complex numbers, compared to the real numbers which are ordered. another issue is with the argument of a complex number, in the polar/exponential form there are infinitely many square roots, however this is not an issue if you pick the principal branch which you basically always do in 4u anyway (or use the cartesian form). generally, i don't think the hsc will care about if you use the quadratic formula or not, and as long as you know you should have two conjugate roots of your polynomial and check this condition to make sure you haven't made any mistakes, this shouldn't be an issue. but, you should also definitely know how to solve through completing the square or other methods, since sometimes they'll ask questions about something like x^4 + x^2 + 1 = 0 in which case the quadratic formula becomes much messier and mistake prone than other methods you could use

 

[pl4smaa21]

u can just say a real number x is negative if x<0 lol. but you're right, you cannot order the complex numbers, compared to the real numbers which are ordered. another issue is with the argument of a complex number, in the polar/exponential form there are infinitely many square roots, however this is not an issue if you pick the principal branch which you basically always do in 4u anyway (or use the cartesian form). generally, i don't think the hsc will care about if you use the quadratic formula or not, and as long as you know you should have two conjugate roots of your polynomial and check this condition to make sure you haven't made any mistakes, this shouldn't be an issue. but, you should also definitely know how to solve through completing the square or other methods, since sometimes they'll ask questions about something like x^4 + x^2 + 1 = 0 in which case the quadratic formula becomes much messier and mistake prone than other methods you could use

yea 100%. I think I developed tunnel vision because I wanted to define negative and positive number using an = sign for some reason lmao, I didn't consider inequalities.(I definitely should have tho cuz its better)

 

[liamkk112]

yea 100%. I think I developed tunnel vision because I wanted to define negative and positive number using an = sign for some reason lmao, I didn't consider inequalities.(I definitely should have tho cuz its better)

it's also circular reasoning to define negative numbers in terms of the absolute value because the absolute value itself is defined based on if a number is negative or positive

 

[pl4smaa21]

it's also circular reasoning to define negative numbers in terms of the absolute value because the absolute value itself is defined based on if a number is negative or positive

tru