Volume of Rotation Question. (Cambridge Ext 1, 12F Q20. ) (1 Viewer)

[ISAM77]

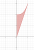
Q20.

c) i: I got wrong, and I disagree with the working out of the solutions book.
ii: I couldn't solve this, and I disagree with the working out of the solutions book.

Just posting this here to see what you guys can do with it Probably an oversight by me; but nonetheless, your help is appreciated.

 

[lqmoney]

I got the same answers as the back of the book so I think the solutions would be correct.
for i: V = which can be expanded and integrated to 15pi/7, your mistake could've been squaring (x^3+2-3x), but if you imagine the final volume as the volume under (x^3+2) minus the volume under 3x, it is clear this is incorrect.

for ii: first expressing both equations with x as the subject, the tangent is given by x=y/3, the cubic equation is given by x=(y-2)^1/3. When determining the volume, we can again split it into two volumes: x=y/3 from 0 to 3 as we are integrating wrt to y, and x=(y-2)^1/3 from 2 to 3 as if we went from 0 to 3 for this term we would include the region in the second quadrant which the question doesn't include.
i.e.

Hope this helps

 

[ISAM77]

I got the same answers as the back of the book so I think the solutions would be correct.
for i: V = which can be expanded and integrated to 15pi/7, your mistake could've been squaring (x^3+2-3x), but if you imagine the final volume as the volume under (x^3+2) minus the volume under 3x, it is clear this is incorrect.

Thanks for answering. Clearly, I'm not understanding something!

for i: We are finding the volume of the solid formed when rotating the shaded region above, about the x axis. Why are you integrating from 1 to 0, instead of 1 to -2?

for ii: I have a similar question. Why are we only looking at the volume of the solid formed by rotating the area in the first quadrant?

I know I must be thinking about this wrong conceptually; I'm just not sure how yet. Pls help!

 

[lqmoney]

In 20. b) you are asked to find the region bounded by the curve, the tangent and the y-axis, which is why we are only concerned with the region from 0 to 1 in i), since the y-axis restricts it to only the first quadrant. It is slightly ambiguous which side of the y-axis we should take the region to be on, but since in a) we are asked about the point x=1, it is reasonable to assume we are only working with the region in Q1. Similar reasoning for ii), so I think your only issue was drawing the wrong region because you forgot to consider that it is bounded by the y-axis.

 

[ISAM77]

In 20. b) you are asked to find the region bounded by the curve, the tangent and the y-axis, which is why we are only concerned with the region from 0 to 1 in i), since the y-axis restricts it to only the first quadrant. It is slightly ambiguous which side of the y-axis we should take the region to be on, but since in a) we are asked about the point x=1, it is reasonable to assume we are only working with the region in Q1. Similar reasoning for ii), so I think your only issue was drawing the wrong region because you forgot to consider that it is bounded by the y-axis.
View attachment 43740

Righto. Seems like I'm clear then. I actually drew the region the same as your at first; but then, that region I posted above was taken directly out of the official Cambridge Worked Solutions as the answer to Q20 b) and I became confused.

Good to know I'm not missing any "big ideas". Thanks very much