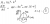Math help (1 Viewer)

[Gtsh]

The amount M of certain medicine present in the blood after t hours is given by M = 9t^2 -t^3 for 0 < t < 9. When is the amount of medicine in the blood increasing most rapidly?

How do I do this? The answer is t=3. I got it from Baulkham hills past paper.

 

[jimmysmith560]

Looking at the above sample solution, it seems that setting the second derivative to equal 0 (i.e. ) would allow you to solve this question. Solving leads to , matching the paper's answer.

I hope this helps!

 

[mmmmmmmmaaaaaaa]

You would need to find the first derivative
which is: 18t-3t^2
Then find when the first derivative equals zero (in this case, t=6)
The final step would be to show that it's a maximum at t=6

 

[Gtsh]

I don't get why we have to use the second derivative. Why can't we use the first derivative, like we would normally do to find the point.
Is it because we are finding when the first derivative is increasing as the question says 'increasing most rapidly'

 

[Gtsh]

You would need to find the first derivative
which is: 18t-3t^2
Then find when the first derivative equals zero (in this case, t=6)
The final step would be to show that it's a maximum at t=6

I thought we had to do this as well

 

[mmmmmmmmaaaaaaa]

I don't get why we have to use the second derivative. Why can't we use the first derivative, like we would normally do to find the point.
Is it because we are finding when the first derivative is increasing as the question says 'increasing most rapidly'

There is two ways to do the final part:
Either a table of values at the first derivative, or use the second derivate
I usually just do the table of values