Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
help with another complex question (1 Viewer)
- Thread starter MAK03
- Start date
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
The first post will be of help for parts i and ii. Part iii will be added later when I had a little bit of thought about it.
part i) Using the properties of a paralleloogram. Already, they have guided you into the question, okay so what do we know about the roots. Have a look at
From what we know the property of a parallelogram goes something like this. Once this is shown now we will complete part i. Here,
Next,
part ii) Ask yourself a question, what is a useful tool from polynomials and part i that we can use to cut out all the noise and immediately show that
Only use the spoilers if you do not know what to do after answering my question
="Use the fact that 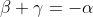 "
"
Sum of Roots
Attachments
-
1.3 MB Views: 2
Last edited:
part iii)
Now we just have to find the roots of the equation, so lets just use the identity from part i and the product of roots to simultaneously solve for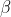 and
and 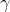 .
.
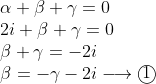
Product of roots
\beta\gamma=-32(1+i)\\(2i)(-4i)\beta\gamma=-32(1+i)\\(8)\beta\gamma=-32(1+i)\\\beta\gamma=-4(1+i)\longrightarrow \textcircled{2})
Now we just sub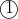 into
into 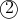
\gamma=-4-4i\\\--\gamma^2-2i\gamma+4+4i=0)
lets use the quadratic formula
^2-4(4+4i)}}{-2}\\\\\gamma=\frac{2i\pm\sqrt{{12-16i}}}{-2}\\\\\gamma=\frac{2i\pm2\sqrt{{3-4i}}}{-2})
Now we can use the identity that the question gave us
}{-2}\\\\\gamma=-2-2i,\ \gamma=2)
So yeah the vertices of the parallelogram are -2-2i, 2, 2i, -4i
Now we just have to find the roots of the equation, so lets just use the identity from part i and the product of roots to simultaneously solve for
Product of roots
Now we just sub
lets use the quadratic formula
Now we can use the identity that the question gave us
So yeah the vertices of the parallelogram are -2-2i, 2, 2i, -4i
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
ExtremelyBoredUser
Bored Uni Student
the emojis are vital for the proof*part iii)
Now we just have to find the roots of the equation, so lets just use the identity from part i and the product of roots to simultaneously solve forand
.
Product of roots
Now we just subinto
lets use the quadratic formula
Now we can use the identity that the question gave us
So yeah the vertices of the parallelogram are -2-2i, 2, 2i, -4i