The symbol |z| means the modulus of z, and thus the length of the vector in the complex plane from the origin to z.
If z is purely real, then this vector lies along the real axis and so the length is the absolute value of z. As such, the absolute value function is the real-value special case of the modulus. Thinking of |z| as an absolute value when z is a non-real complex number is unhelpful because it is the absolute value that is the special case of a more general property, even though they are necessarily taught in the reverse order.
Since where
where 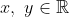 is a vector from
is a vector from  to
to  , it can be broken into perpendicular component vectors
, it can be broken into perpendicular component vectors  parallel to the real axis and
parallel to the real axis and 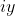 parallel to the imaginary axis. Applying Pythagoras' Theorem shows that
parallel to the imaginary axis. Applying Pythagoras' Theorem shows that
} \\ &= |x|^2 + |i|^2|y|^2 \qquad \qquad \text{as $|z_1z_2| = |z_1||z_2|$} \\ &= |x|^2 + 1^2 \times |y|^2 \qquad \qquad \text{as $|i| = 1$} \\ &= x^2 + y^2 \qquad \qquad \text{as, for $k \in \mathbb{R}$, $|k|^2= k^2$, and as $x,\ y \in \mathbb{R}$ by definition} \end{align*})
Looking at the complex conjugates, we can see that
 \times \big(\,\overline{x + iy}\,\big) \\&= (x + iy)(x - iy) \\ &= x^2 + ixy - ixy - i^2y^2 \\ &= x^2 - (-1)y^2 \qquad \qquad \text{as $i^2 = -1$} \\ &= x^2 + y^2 \\ &= |z|^2 \end{align*})
If z is purely real, then this vector lies along the real axis and so the length is the absolute value of z. As such, the absolute value function is the real-value special case of the modulus. Thinking of |z| as an absolute value when z is a non-real complex number is unhelpful because it is the absolute value that is the special case of a more general property, even though they are necessarily taught in the reverse order.
Since
Looking at the complex conjugates, we can see that
