Complex no. (1 Viewer)
- Thread starter =)(=
- Start date
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
For this question, this is how I would see it z and its conjugate gives 5 automatically this should tell us that
Doing simultaneous equations
We see quickly that
Thus,
Disclaimer. The fraction gave us a squared value so already you are doing a "find the square roots of a+ib," type of question.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
I reckon this should beLet
It follows that
If
then
If
then(by multiplying using conjugates)
So
Finally, simulatenously solveand
I'll leave that final part as an exercise to you.
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 339
- Gender
- Male
- HSC
- 2022
That's true, its' edited now.I reckon this should be. One little mistake yet a vital one.
Interestingly, by making the same mistake twice I still got the correct solution lol.
I have another one slightly more difficult, part b please
View attachment 32903
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
This questionI have another one slightly more difficult, part b please
View attachment 32903
how did you get the -2Re(a)z term ?
Conjugates.
ohh i get it because the conjugates are identical to the original, so its just z(2a), would you have to put Re(a) since it said the coefficents were real in the q?This question
Conjugates.
ExtremelyBoredUser
Bored Uni Student
I mean you could do it algebraically to convince yourself.ohh i get it because the conjugates are identical to the original, so its just z(2a), would you have to put Re(a) since it said the coefficents were real in the q?
let a be a complex number, a+ib. a conjugate is simply a - ib.
a + ib + a - ib = 2a
and 2a is simply double the real component of a complex number, a + ib "2Re(a)". It would be considered a coefficient since you would have factored it from z.
ohh i get, is it because re(a) is just a since that is the real component of a?I mean you could do it algebraically to convince yourself.
let a be a complex number, a+ib. a conjugate is simply a - ib.
a + ib + a - ib = 2a
and 2a is simply double the real component of a complex number, a + ib "2Re(a)". It would be considered a coefficient since you would have factored it from z.
Note that the question is flawed.
The quadratic equation with roots at and
and 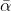 , where
, where  is a complex number with a non-zeo imaginary part is
is a complex number with a non-zeo imaginary part is
(z - \bar{\alpha}) = z^2 - 2z\Re{(\alpha)} + \alpha\bar{\alpha} = z^2 - 2z\Re{(\alpha)} + |\alpha|^2 = 0)
but the question has the constant term as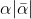 , which is a non-real complex number as
, which is a non-real complex number as 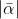 is a real constant.
is a real constant.
I am sure the question is seeking one of the above equations but, as written, it is impossible.
The quadratic equation with roots at
but the question has the constant term as
I am sure the question is seeking one of the above equations but, as written, it is impossible.
ohh i get, is it because re(a) is just a since that is the real component of a?
ohh makes sense i got mixed up between a and alpha
ExtremelyBoredUser
Bored Uni Student
if thats the case then try using x+iy or any other variables that are more distinguishable so you don't subconsciously interpret one variable as another unless specified.ohh makes sense i got mixed up between a and alpha
Yes, I wondered if that might be the case, hence my clarification after I noticed the definitionohh makes sense i got mixed up between a and alpha
let a be a complex number, a+ib. a conjugate is simply a - ib.
ExtremelyBoredUser
Bored Uni Student
They're the same thing.i was also wondering why does z multiplied by its conjugate give the absolute value of z ^2, shouldn't it just be x^2 + y^2?
You can see;
where z is a complex number x + iy.


