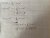-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
sryy another binomial q help plss (1 Viewer)
- Thread starter yashbb
- Start date
but then what do i do with the r=1, do i start with that as the first term?
tickboom
Member
- Joined
- Aug 21, 2020
- Messages
- 72
- Gender
- Male
- HSC
- 2001
- Uni Grad
- 2008
Oh actually I think there’s still an issue with the x^r instead of x^(r-1) on the RHS … hmmmm
yes that was what i was wondering.... i have no clue.
tickboom
Member
- Joined
- Aug 21, 2020
- Messages
- 72
- Gender
- Male
- HSC
- 2001
- Uni Grad
- 2008
yeah sorry I think differentiation isn’t the way to go …
then do you have any other suggesstions?yeah sorry I think differentiation isn’t the way to go …
yea same, ok thank you though!!!
OH YES THIS MAKES SO MUCH SENSE, THANK YOU SO MUCH.
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,101
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Maybe create one thread dedicated to just binomial questions whenever you have a question you can post them there.
Last edited:
Perhaps easier to see without the sigma notation:
^{n-1})
I can re-write this theorem as:
\binom{n}{n-1}x^{n-1} + n\binom{n}{n}x^n = nx(1+x)^{n-1} \qquad \qquad \text{. . . . . . . . . (*)})
Now, we are given that:
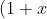^n = \binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + ... + \binom{n}{n-1}x^{n-1} + \binom{n}{n}x^n \qquad \qquad \text{. . . . . . . . . . (**)})
}\big]$}\ &= \cfrac{d}{dx}\bigg[(1+x)^n\bigg] \\ &=n\bigg[(1+x)^{n-1}\bigg] \times \cfrac{d}{dx}\big(1+x\big) \qquad \text{by using the Chain Rule} \\ &= n\bigg[(1+x)^{n-1}\bigg] \times (0 + 1) \\ &= n(1+x)^{n-1} \end{align*})
}\big]$}\ &= \cfrac{d}{dx}\bigg[\binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + ... + \binom{n}{n-1}x^{n-1} + \binom{n}{n}x^n\bigg]\\ &= \binom{n}{1} \times 1 + \binom{n}{2}\times 2x + ... + \binom{n}{n-1}\times (n-1)x^{n-2} + \binom{n}{n} \times nx^{n-1} \quad \text{by term-by-term differentiation} \\ &= \binom{n}{1} + 2\binom{n}{2}x + ... + (n-1)\binom{n}{n-1}x^{n-2} + n\binom{n}{n}x^{n-1} \end{align*})
}\ &=\ \text{RHS of (**)} \\ \text{and it follows that} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \cfrac{d}{dx}\big[\text{LHS of (**)}\big] &= \cfrac{d}{dx}\big[\text{RHS of (**)}\big] \\ \text{we have demonstrated that} \qquad \binom{n}{1} + 2\binom{n}{2}x + ... + (n-1)\binom{n}{n-1}x^{n-2} + n\binom{n}{n}x^{n-1} &= n(1+x)^{n-1} \\ \\ \text{Multiplying by $x$ gives:} \qquad \binom{n}{1}x + 2\binom{n}{2}x^2 + ... + (n-1)\binom{n}{n-1}x^{n-1} + n\binom{n}{n}x^n &= nx(1+x)^{n-1} \qquad \text{which is the required result (*)} \\ \text{And thus,} \qquad \sum_{r=1}^n \binom{n}{r}rx^r = nx(1+x)^{n-1} \end{align*})
A minor quibble with @tickboom's approach, mostly for the sake of MX2 students... saying that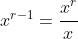 
, which is effectively the calculation
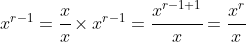
involves the implicit assumption that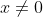
, because you can't divide by zero. Thus, Tickboom's proof has actually shown that
^{n-1} \qquad \qquad \text{for all real $x \ne 0$})
and to be completed, needs the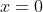
case to be addressed separately. Now, that case is trivial in that it has LHS = 0 and RHS = 0, and would quite likely be ignored in an MX1 question... but in an MX2 question under the proof topic, some markers would note that the proof was incomplete. My proof, above, does not have any such problem as it multiplies by 
rather than dividing. It is true that multiplying by 0 must be done with caution (as it can take a false statement and produce a true one), but in this case, it is taking a statement that is known to be true, in which case multiplying by any 
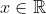(including 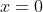) will not produce a false statement, and so the proof covers all real . Note also that my proof could be written more concisely... I have separated the differentiation steps to make what is happening clearer and more explanatory... I would write a briefer proof in an exam situation, something like:
I can re-write this theorem as:
Starting from the given binomial expansion:
^n \\ \text{And so} \qquad \cfrac{d}{dx}\bigg[\binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + ... + \binom{n}{n-1}x^{n-1} + \binom{n}{n}x^n\bigg] &= \cfrac{d}{dx}\bigg[(1+x)^n\bigg] \\ 0 + \binom{n}{1} + 2\binom{n}{2}x + ... + (n-1)\binom{n}{n-1}x^{n-2} + n\binom{n}{n}x^{n-1}&= n(1+x)^{n-1} \\ \text{Multiplying by $x$ gives:} \qquad \binom{n}{1}x + 2\binom{n}{2}x^2 + ... + (n-1)\binom{n}{n-1}x^{n-1} + n\binom{n}{n}x^n &= nx(1+x)^{n-1} \qquad \text{which is the required result (*)} \\ \text{And thus,} \qquad \sum_{r=1}^n \binom{n}{r}rx^r = nx(1+x)^{n-1} \end{align*})
An Alternative Proof
Anyone familiar with the standard proof might recognise, or notice from the result on RHS of the theorem, that there is an extra. So , start with:
^n \qquad \text{. . . . . . . . . . (A))
and, by multiplying by:
^n \qquad \text{. . . . . . . . . . (B))
^n\bigg] &= (1+x)^n \times 1 + x \times n(1+x)^{n-1} \qquad \text{(Product Rule)} \\ \cfrac{d}{dx}\bigg[x(1+x)^n\bigg] - (1+x)^n &= nx(1+x)^{n-1} \qquad \text{recognising that the RHS is $x$ times the RHS of our Theorem} \end{align*})
^{n-1} \\ &= \cfrac{d}{dx}\bigg[x(1+x)^n\bigg] - (1+x)^n \\ &= \cfrac{d}{dx}\bigg[\text{RHS of (B)}\bigg] - (1+x)^n \\ &= \bigg[\binom{n}{0} + 2\binom{n}{1}x + 3\binom{n}{2}x^2 + ... + n\binom{n}{n-1}x^{n-1} + (n+1)\binom{n}{n}x^n\bigg] - (1+x)^n \qquad \text{differentiating (B)} \\ &= \bigg[\binom{n}{0} + 2\binom{n}{1}x + 3\binom{n}{2}x^2 + ... + n\binom{n}{n-1}x^{n-1} + (n+1)\binom{n}{n}x^n\bigg] \\ &\qquad -\bigg[\binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + ... + \binom{n}{n-1}x^{n-1} + \binom{n}{n}x^n\bigg] \qquad \text{substituting (A)} \end{align*})
\binom{n}{n} - \binom{n}{n}\bigg]x^n \\ &= \binom{n}{1}x + 2\binom{n}{2}x^2 + ... + (n-1)\binom{n}{1}x^{n-1} + n\binom{n}{n}x^n \\ &= x\bigg[\binom{n}{1} + 2\binom{n}{2}x + ... + (n-1)\binom{n}{1}x^{n-2} + n\binom{n}{n}x^{n-1}\bigg] \end{align*})
We have thus established that:
\binom{n}{1}x^{n-2} + n\binom{n}{n}x^{n-1}\bigg] = nx(1+x)^{n-1})
And thus know that either 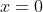or we have our required result...
I can re-write this theorem as:
Now, we are given that:
involves the implicit assumption that
and to be completed, needs the
I can re-write this theorem as:
Starting from the given binomial expansion:
An Alternative Proof
Anyone familiar with the standard proof might recognise, or notice from the result on RHS of the theorem, that there is an extra
and, by multiplying by
We have thus established that:
how would i go about doing that.
THANK YOUUUUPerhaps easier to see without the sigma notation:
I can re-write this theorem as:
Now, we are given that:
A minor quibble with @tickboom's approach, mostly for the sake of MX2 students... saying that
involves the implicit assumption that
and to be completed, needs the
I can re-write this theorem as:
Starting from the given binomial expansion:
An Alternative Proof
Anyone familiar with the standard proof might recognise, or notice from the result on RHS of the theorem, that there is an extra
and, by multiplying by
We have thus established that:
And thus know that either
Whats the purpose of the second line?
I think that sigma notation is extension 2 now. Nesa writes " Sigma notation is formally introduced in the Mathematics Extension 2 course in the topic MEX-P2: Further Proof by Mathematical Induction. ". You need to still be able to do this question though - I recognize it from a yearly paper I can't remember which though.
tickboom
Member
- Joined
- Aug 21, 2020
- Messages
- 72
- Gender
- Male
- HSC
- 2001
- Uni Grad
- 2008
The second line differentiates both sides wrt x. The purpose of doing that is to get the exponents to match what we are being asked to prove.
ohh sorry i mean the second last one where you have 0+...
tickboom
Member
- Joined
- Aug 21, 2020
- Messages
- 72
- Gender
- Male
- HSC
- 2001
- Uni Grad
- 2008
ohhhh … that step is to show why you can start the summation from r=1 instead of r=0 (notice the subtle difference in where the sigma starts).