Trigonometric Functions and Graphs Fitzpatrick Questions (1 Viewer)
- Thread starter frankfurt
- Start date
mikikieko12
Member
- Joined
- Jun 11, 2018
- Messages
- 28
- Gender
- Undisclosed
- HSC
- 2020
- Uni Grad
- 2024
An alternate method:
Attachments
-
395.8 KB Views: 35
mikikieko12
Member
- Joined
- Jun 11, 2018
- Messages
- 28
- Gender
- Undisclosed
- HSC
- 2020
- Uni Grad
- 2024
I checked the solutions in Pearson textbook. They are correct.Solution very nicely set out and handwriting really neat.
But not sure if your answers fully correct.
Damn this is so much cleanerAn alternate method:
Hi,
yeah that's the solution
thanks!
CoolKids101
New Member
For (a) and (b), you can either use t-formula or auxiliary angles, but not sure if they are in 2U. For (c), try converting sec and tan to cos and sine and then simplify, and for (d) simply use your double angle formula's and simplifyThanks everyone,
Do guys know how to do these ones as well? They're from the same textbook, Fitzpatrick, Exercise 12.2 Question 7
View attachment 28812
There were some other ones I didn't understand from this chapter either, could you please help me out with these ones too?
From Exercise 12.3:
Question 7

Question 8

From Exercise 12.4:
Question 2.e (I've attached the entire question for convenience)

Question 7.c and d (I've attached the entire question for convenience)

From the Chapter Review:
Question 1

Question 7

Thanks again in advance
From Exercise 12.3:
Question 7

Question 8

From Exercise 12.4:
Question 2.e (I've attached the entire question for convenience)

Question 7.c and d (I've attached the entire question for convenience)

From the Chapter Review:
Question 1

Question 7

Thanks again in advance
mikikieko12
Member
- Joined
- Jun 11, 2018
- Messages
- 28
- Gender
- Undisclosed
- HSC
- 2020
- Uni Grad
- 2024
Worked Solutions from Textbook:Thanks everyone,
Do guys know how to do these ones as well? They're from the same textbook, Fitzpatrick, Exercise 12.2 Question 7
View attachment 28812


Pretty sure that T-formula and auxiliary angles are in 3u but I was wondering if there was a way to solve this question using 2u contentFor (a) and (b), you can either use t-formula or auxiliary angles, but not sure if they are in 2U. For (c), try converting sec and tan to cos and sine and then simplify, and for (d) simply use your double angle formula's and simplify
mikikieko12
Member
- Joined
- Jun 11, 2018
- Messages
- 28
- Gender
- Undisclosed
- HSC
- 2020
- Uni Grad
- 2024
I only have worked solutions for every odd question, here are the ones from the textbook for odd questions:There were some other ones I didn't understand from this chapter either, could you please help me out with these ones too?
From Exercise 12.3:
Question 7
View attachment 28813
Question 8
View attachment 28814
From Exercise 12.4:
Question 2.e (I've attached the entire question for convenience)
View attachment 28815
Question 7.c and d (I've attached the entire question for convenience)
View attachment 28816
From the Chapter Review:
Question 1
View attachment 28817
Question 7
View attachment 28818
Thanks again in advance
12.3
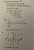
12.4

Chapter Review

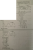
for (a), divide both sides by cosx, then square both sides, use the identity tan^2(x)+1=sec^2(x) to get the equation in terms of tan^2(x), then solve as usual. This method can be applied to all of 7. (note this may give extra solutions plug back in to verify, and also it may miss some solutions, nothing you can do).Thanks everyone,
Do guys know how to do these ones as well? They're from the same textbook, Fitzpatrick, Exercise 12.2 Question 7
View attachment 28812



