You are right, we don't.
Take the point at the top of the building and closest to the point of projection as
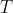
. Taking the projection as from
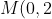)
, then
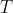
is
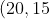)
. If we require the projectile to pass through
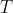
, we will get a quadratic equation in

that yields two angles,
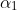
and
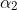
where
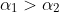
. Firing the projectile at
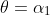
corresponds to the given diagram, with the projectile rising to a maximum height and then passing through
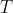
on its descent. Firing at
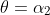
corresponds to the projectile passing through
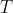
as it ascends and then continuing on to reach its maximum height. For any angle
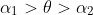
, when the projectile has travelled a distance of
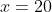
m horizontally, it will have a height
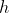
such that it is some distance above the leading edge of the building,
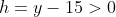
.
If we assume that the depth / width of the building in our horizontal direction is great relative to the scale of the motion, any angle
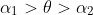
will result in a roof landing. If it is not, then you are correct, the angle needs to be further constrained to ensure a roof landing, but we also need further information to find a solution.
If you think it is appropriate, you could examine what is the maximum possible range for a landing on the roof and then consider whether this is reasonable for a roof size. You could also examine whether the angles near
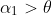
or those near
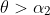
will land closest to
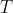
and thus would be safer choices for a roof landing.


