2. A man in a rowing boat is presently 6km from the nearest point A on the shore. He wants to reach as soon as possible a point B that is a further 20km down from the shore from A. If he can row at 8km/hr and run at 10km/hr , how far from A should he land.
Firstly, let's look at the answer that is sought:
Let
S be the starting point for the rowing boat, which is 6 km from point
A on the shore, which is the closest point on the shore to
S.. We know that
B is 20 km from
A along the shore, and let point
P be located a distance of x km from A, so that the distance
PB is (20 -
x) km.
The attached file contains this information shown in a diagram. We seek the position of
P (and thus the value of
x) so as to minimise the travel time from
S to
B. Let
T be the travel time (in hours) from
S to
B, made up of the travel time from
S to
P (
tSP) and the travel time from
P to
B (
tPB). In otherwise, we need to minmise:
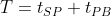
Defining the distances SP and PB (in km) as
dSP and
dPB, respectively, and remembering that distance equals speed times times, we can see that:

Now, applying Pythagoras' Theorem to triangle
SAP, we can see that
SA2 +
AP2 =
SP2:
^{\frac{-1}{2}} \times (2x + 0) \\ &= \frac{-1}{10} + \frac{2x}{8 \times 2} \times \frac{1}{\sqrt{x^2 + 36}} \\ &= \frac{-1}{10} + \frac{x}{8\sqrt{x^2 + 36}} \end{align*})
To find stationary points, we need to set this derivative to zero:
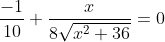
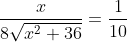
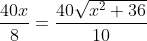

)
x^2 = 16 \times 36 \implies x^2 = \frac{16 \times 4 \times 9}{9} = 64)
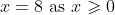
So, there is a stationary point at (
x = 8 km,
T = 2 h 27 min)
Following the path
SAB (corresponding to
x = 0), the rower rows 6 km taking 45 min and then runs 20 km taking 2 h, so that T = 2 h 45 min.
Following path SB (rowing directly from S to B, corresponding to
x = 20), the distance rowed is (6
2 + 20
2)
0.5 = 20.8806... km taking a little over 2 h 36 min. It follows that the stationary point is a minimum, and thus the rower should row to point
P, 8 km from
A towards
B.
Of course, that
x = 8 corresponds to a minimum can also be established by the usual methods of examining the behaviour of
dT/dx in the vicinity of
x = 8 or by showing that the second derivative is positive.
Note, however, that we have assumed that the shore line from
A to
B is a straight line with
AB perpendicular to
AS. I believe that this is what is intended, but the question does not actually specify this and if the shoreline is different from this then the answer may change.
