stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
For this integral, some trig identities may make your life easier. Of course, Weierstrass substitution will also work.
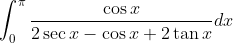
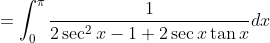
^2}dx)
^2dx)
dx)
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
It seems no one has attempted yet. This one is a little bit interesting.#83 and #88 are still outstanding and this is a new one.
Feel free to share your attempt.
+16^{2x}-5\left(4^{3x}\right)}+\sqrt[3]{2^{10x}-2^{8x+1}}\right)dx)
Where are you pulling these questions from?New integral:
^x\right)}{x^2\sin^2x+\cos^2x+x\sin2x}dx=\frac{4-\pi}{4+\pi}\cdot\frac{\ln\pi}{\ln3})
New integral:
^x\right)}{x^2\sin^2x+\cos^2x+x\sin2x}dx=\frac{4-\pi}{4+\pi}\cdot\frac{\ln\pi}{\ln3})
I'll leave the intended solution for someone else to write out (p.s I think you need to be a bit careful about the first part, the integrals are indefinite so equality will only hold up to a constant as written.)For, let
Prove that
Given that
Show that
^n \, dx = \sum_{k=0}^n (-1)^k k!\binom{n}{k}.)
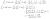
Yep, works super well for these integrals with logs.is that Leibnitz?
