Combination (1 Viewer)

[HeroWise]

Need help with this comb question

Part i is fine but my answer of part ii isnt matching with the book,

 

[fan96]

Case 1: B is not included. Then, you have to select the whole committee from nine others (without restriction).

There are choices.

Case 2: B is included. Now, we have to select five more people from nine. But A is one of the nine, and we cannot select A. Therefore we must select our five from the remaining eight people.

There are choices.



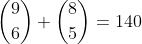
Is that the answer?

 

[HeroWise]

Answer states 140

Im kinda confused with something;
I got Case 2: But Case 1 is causing me issues
Case 1: What i did was i made "A" Included rather than B excluded which sounds like the same thing but when you do it

You have 8C5 comb? Because its guaranteed for 1 A so (10-1=9) which is 9 and B cant be in with A so 8 Choices. And when A fill in a spot There are 5 more spots left
8C5 Im misinterpreting the question ; If u can pls clarify.

And anyway 9C5 is correct and I understand why you did it, but can you explain why I went wrong

 

[HeroWise]

This question is also causing some probs for me

Im getting wayyyy offf for this

THe answer for this states 73080

 

[fan96]

Case 1: What i did was i made "A" Included rather than B excluded which sounds like the same thing but when you do it

You have 8C5 comb? Because its guaranteed for 1 A so (10-1=9) which is 9 and B cant be in with A so 8 Choices. And when A fill in a spot There are 5 more spots left
8C5

That's correct. I'm not sure what your mistake is because if you did that then you should have arrived at the right answer.

The restriction is, essentially, that A and B cannot both be on the committee. You can have either one or the other but not both. A or B but not AB.

If you were to split the problem into cases in terms of "including A" then you would have:

Case 1: A is included. Then, B cannot be on the committee. You have five more spots to fill and two candidates have been eliminated so you get .

Case 2: A is not included. There are no further restrictions here so you simply get .

This question is also causing some probs for me

Im getting wayyyy offf for this

THe answer for this states 73080

We need exactly one independent, at least three liberal and at least one labor. We can break this up into three cases and calculate individually:

1 Ind 3 Lib 3 Lab


1 Ind 4 Lib 2 Lab


1 Ind 5 Lib 1 Lab




If you are faced with a problem where counting all the cases would not be viable, you might be able to take the complementary case instead. e.g. instead of "at least two" you could consider "one or zero" and subtract it from the number of permutations/combinations with no restrictions.

 

[HeroWise]

i did A included B included v_v as my two cases|


EDIT: Thanks a lot for the second question i see where i made my mistake. I had 1 Ind 3 lib and 1 lab and 2 "rand" LOL I see what teh question actually menant