-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
MATH2901 Higher Theory of Statistics (1 Viewer)
- Thread starter leehuan
- Start date
We can just prove it by cases: either X ≥ Y occurs or Y > X occurs, and in either case the LHS is ≥ 0, since f and g are increasing functions.
Same is true (replacing X by x and Y by y) if x and y are just real numbers in the domain of f and g if f and g are functions defined on a subset of the reals.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
No, it was a function of a random variable. But InteGrand's solution worked.I can't make sense out of the question.
Is it meant to be (RTP):
 - f(Y))(g(X) - g(Y))\geq 0) = 1)
_______________________________________
Whilst I get why chisq is the result of Z^2 (Z~N(0,1)), where in practice does it actually get used? What's so powerful about the square of the standard normal?
The point I'm making is that how can a random variable exist alone without specification of it's probability?No, it was a function of a random variable. But InteGrand's solution worked.
Example, X is gamma random variable with whatever parameters. Prove that X > 0. How does this make sense? It should be prove that P(X > 0) = 1.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Look at the 2014 finals. I'm sure you still have it from back when you did the course.The point I'm making is that how can a random variable exist alone without specification of it's probability?
Example, X is gamma random variable with whatever parameters. Prove that X > 0. How does this make sense? It should be prove that P(X > 0) = 1.
I don't even care about the distribution of X in this question. I just care that X is a random variable. And I want to find something about f(X), which is what the function does to the random variable (given that f is monotonic increasing).
It's used in many hypothesis tests, for example.No, it was a function of a random variable. But InteGrand's solution worked.
_______________________________________
Whilst I get why chisq is the result of Z^2 (Z~N(0,1)), where in practice does it actually get used? What's so powerful about the square of the standard normal?
Look at another simple example.Look at the 2014 finals. I'm sure you still have it from back when you did the course.
I don't even care about the distribution of X in this question. I just care that X is a random variable. And I want to find something about f(X), which is what the function does to the random variable (given that f is monotonic increasing).
Define f: R -> R such that f(x) = x^2 and let X be a random variable with gamma distribution, say. Prove that f(X) = X^2 > 0.
It's obvious that this is true because you're just squaring positive random variables and they stay positive. But how does it make sense alone? It should be prove that P(X^2 > 0) = 1.
The point is, random variables cannot exist alone. It needs to be associated with probabilities.
- Joined
- Feb 16, 2005
- Messages
- 8,385
- Gender
- Male
- HSC
- 2006
It gets used a lot to understand variances and forms the basis of other distributions such as the F-distribution (which has obvious applications in ANOVA, regression etc)Whilst I get why chisq is the result of Z^2 (Z~N(0,1)), where in practice does it actually get used? What's so powerful about the square of the standard normal?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
It makes perfect sense to me after seeing the earlier question. And again, I couldn't care less if it's normal or gamma or exponential or a discrete r.v.Look at another simple example.
Define f: R -> R such that f(x) = x^2 and let X be a random variable with gamma distribution, say. Prove that f(X) = X^2 > 0.
It's obvious that this is true because you're just squaring positive random variables and they stay positive. But how does it make sense alone? It should be prove that P(X^2 > 0) = 1.
The point is, random variables cannot exist alone. It needs to be associated with probabilities.
You've done the course before. If you're dissatisfied, pick up the exam paper and take it up with the lecturer.
It might be an abuse of notation. But otherwise I don't see what's wrong with it.
By the way, this is a Pareto Distribution with scale parameter 1 (and shape parameter alpha). This distribution is related to the "80-20" law or "Pareto principle", which you may have heard of.MInd blanking.
 Find an expression for }\mathbb{E}[X\mid X > x_{0.8}])
A fact about Pareto distributions is that the conditional distribution of a Pareto r.v. X given the event that X is greater than a given number b (where b is greater than or equal to the scale parameter of the distribution) is still a Pareto distribution, with the same shape parameter but with new scale parameter b. Using this fact and the formula for the mean of a Pareto distribution, the desired conditional mean can be deduced.
(These facts are facts that should be proved before being used for this Q. I suppose, and can be all proven as an exercise using standard methods for dealing with truncated distributions. For this particular Q., you wouldn't need to know these facts, you could just do the Q. normally, but they are interesting and it is what the Q. was probably getting at (particularly the 80-20 law, which is maybe why they chose the 80-th percentile), so I included them here.)
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
For my reference sake, does the 2,2 entry of the inverse approximate Var(\hat{\beta})?
Edit: Oops.
Last edited:
For my reference sake, does the 2,2 entry of the inverse approximate \hat{\beta}?
I think double check your Var, the beta terms should end up cancelling out I think.Hang on, I'm not sure if I'm doing something wrong because I run into a circular argument.
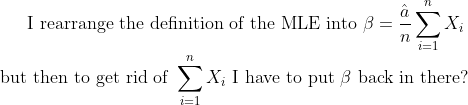
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Oh. My bad. I didn't do 1/detI think double check your Var, the beta terms should end up cancelling out I think.

