Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
ACTL1101 Questions Help (mostly first year uni probability) (1 Viewer)
- Thread starter 1008
- Start date
Hi
I am doing ACTL1101 at UNSW this semester, so I'd like to ask a few first year probability questions here:
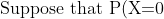=1 - P(X=1). If E(X) = 3Var(X), find P(X=0).})
Last edited:
I think there are typos here because the sums don't really make sense. (I presume i was meant to be a summation index, but it appears in the limits of summation too, which a summation index should never do. Also, r hasn't been defined I think.)Thanks

I guess the first sum should just say that the sum over all i of n_i is m. (I.e. Total no. of families is m.) In fact, for both sums, the sums are just over all values of i.
Last edited:
I checked but I couldn't find any errors/typos I've made. I think you can assume r to be the highest number of children in one single family.I think there are typos here because the sums don't really make sense. (I presume i was meant to be a summation index, but it appears in the limits of summation too, which a summation index should never do. Also, r hasn't been defined I think.)
I guess the first sum should just say that the sum over all i of n_i is m. (I.e. Total no. of families is m.)
Don't worry, I think I've figured out what the Q. is asking. If you haven't made a typo, then the Q. itself essentially has a typo I think, because i is meant to be the thing we're summing over, yet it appears as the lower limit of a sum, which cannot happen.I checked but I couldn't find any errors/typos I've made. I think you can assume r to be the highest number of children in one single family.
Here are some hints for a method:
• For any given i, find an expression for Pr(X = i), i.e. The probability that the randomly chosen family is a family with i children. This expression is very simple and easy to find once you understand the notation used.
• Thus, write down an expression for E[X] using the definition of expectation for discrete r.v.'s.
• Repeat the above two steps for Y (again, this is very simple to do once you've gotten your head around the notation).
• Using your expressions for E[Y] and E[X], derive the required inequality (it shouldn't be too hard to do once you have the expressions).
• For any given i, find an expression for Pr(X = i), i.e. The probability that the randomly chosen family is a family with i children. This expression is very simple and easy to find once you understand the notation used.
• Thus, write down an expression for E[X] using the definition of expectation for discrete r.v.'s.
• Repeat the above two steps for Y (again, this is very simple to do once you've gotten your head around the notation).
• Using your expressions for E[Y] and E[X], derive the required inequality (it shouldn't be too hard to do once you have the expressions).
Alright thanks for that, will look into it tomorrow and will let you know how I went.Here are some hints for a method:
• For any given i, find an expression for Pr(X = i), i.e. The probability that the randomly chosen family is a family with i children. This expression is very simple and easy to find once you understand the notation used.
• Thus, write down an expression for E[X] using the definition of expectation for discrete r.v.'s.
• Repeat the above two steps for Y (again, this is very simple to do once you've gotten your head around the notation).
• Using your expressions for E[Y] and E[X], derive the required inequality (it shouldn't be too hard to do once you have the expressions).
One of my friends asked me...I have no idea where he got it from...Where are these questions from?
Oh and yeah thanks I figured it out...Here are some hints for a method:
• For any given i, find an expression for Pr(X = i), i.e. The probability that the randomly chosen family is a family with i children. This expression is very simple and easy to find once you understand the notation used.
• Thus, write down an expression for E[X] using the definition of expectation for discrete r.v.'s.
• Repeat the above two steps for Y (again, this is very simple to do once you've gotten your head around the notation).
• Using your expressions for E[Y] and E[X], derive the required inequality (it shouldn't be too hard to do once you have the expressions).
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015

Something's weird...
Just by inspection I could tell that the expectation for the second case would be higher than the first. But why should I not be surprised that the variances are the exact same?
I have a feeling this isn't just by coincidence...
Last edited:
Note that A = 25000 – B, where A is the r.v. describing the value from investment A, and similarly for B.
Something's weird...
Just by inspection I could tell that the expectation for the second case would be higher than the first. But why should I not be surprised that the variances are the exact same?
I have a feeling this isn't just by coincidence...
Therefore, by properties of variance (namely that an additive constant doesn't change the variance, and neither does the presence of a multiplicative factor of -1), we have
Var(A) = Var(25000 – B) = Var(B).
Yeah that's a true statement (assuming those are independent r.v.'s). That says that a sum of independent Poisson random variables is Poisson with rate parameter equal to the sum of the original rate parameters. It was proved by leehuan as an old homework exercise I believe (but the proof isn't written up here): http://community.boredofstudies.org...theorem-normal-distributions.html#post7161430 .Is it true that:
If so, what theorem is it?
Last edited:
If you want to actually see a proof, you can find one here: http://math.stackexchange.com/quest...f-sum-of-two-random-independent-variables-x-y .
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Please explain where their product came from? 
Company NewGen has one electirc generator that has five components. All five components are required to work to produce electricity. The time until failure for each component follows an exponential distribution with mean 10. The times until failure for the five components are independent.
What is the expected value of the time that the generator produces electricity.

Company NewGen has one electirc generator that has five components. All five components are required to work to produce electricity. The time until failure for each component follows an exponential distribution with mean 10. The times until failure for the five components are independent.
What is the expected value of the time that the generator produces electricity.

Please explain where their product came from?
Company NewGen has one electirc generator that has five components. All five components are required to work to produce electricity. The time until failure for each component follows an exponential distribution with mean 10. The times until failure for the five components are independent.
What is the expected value of the time that the generator produces electricity.

Last edited:

