Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Interesting mathematical statements (1 Viewer)
- Thread starter Paradoxica
- Start date
Paradoxica
-insert title here-
that's not very interesting.
it's a fairly trivial consequence of Stirling's Approximation... and Limits...
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Too bad, cause even simple things like the power series for exp are interesting when you first see it.
(Also it was not a consequence in my homework. It was an intermediate step to GET to Stirling's approximation)
(Also it was not a consequence in my homework. It was an intermediate step to GET to Stirling's approximation)
Paradoxica
-insert title here-
I know. But I'm not the one doing it, so ¯\_(ツ)_/¯Too bad, cause even simple things like the power series for exp are interesting when you first see it.
(Also it was not a consequence in my homework. It was an intermediate step to GET to Stirling's approximation)
sida1049
Well-Known Member
- Joined
- Jun 18, 2013
- Messages
- 925
- Gender
- Male
- HSC
- 2015
It is as if you're trying to make our boys Uri and Daniel proud at the same time
the expression:
( (i0*(1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1)))) + (i1*(1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1)))) + (i2*(1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1)))) + (i3*(1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1)))) + (i4*(1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))))/(0+1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1))+1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1))+1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1))+1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1))+1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))
is equal to the largest positive integer(and 0) out of i0,i1,i2,i3,i4.
"a/b" denotes floor(a/b) or integer division
"a%b" denotes a mod b
"a+b" and "a*b" is obvious
generated through a python script. I realised that it's not the shortest way to express such a thing, but still. The most efficient expression would still take up acouple lines(i would think). I encourage other people to try to write an expression that is equal to the largest of two numbers using only these operations.
( (i0*(1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1)))) + (i1*(1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1)))) + (i2*(1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1)))) + (i3*(1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1)))) + (i4*(1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))))/(0+1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1))+1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1))+1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1))+1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1))+1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))
is equal to the largest positive integer(and 0) out of i0,i1,i2,i3,i4.
"a/b" denotes floor(a/b) or integer division
"a%b" denotes a mod b
"a+b" and "a*b" is obvious
generated through a python script. I realised that it's not the shortest way to express such a thing, but still. The most efficient expression would still take up acouple lines(i would think). I encourage other people to try to write an expression that is equal to the largest of two numbers using only these operations.
The principle of duality in the real projective plane is quite a beautiful result.
It's a stunning example of how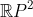 "removes the imperfections" from
"removes the imperfections" from 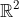 .
.
(To put it informally, the real projective plane is the union of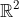 and a "line at infinity", with the property that parallel lines intersect on the "line at infinity".)
and a "line at infinity", with the property that parallel lines intersect on the "line at infinity".)
The principle of duality says that any theorem involving points and lines in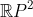 is still true if you replace "point" with "line" and vice versa.
is still true if you replace "point" with "line" and vice versa.
And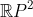 has more interesting properties, e.g. the fact that all non-degenerate conic sections are projectively equivalent.
has more interesting properties, e.g. the fact that all non-degenerate conic sections are projectively equivalent.
It's a stunning example of how
(To put it informally, the real projective plane is the union of
The principle of duality says that any theorem involving points and lines in
And
Arrowshaft
Well-Known Member
for fast enough
Writing a and b is a crime in itself
for fast enoughand
.
