A much easier method is to notice that any 2x2x2 cube has a vertex (at the centre) which is common for all 8 cubes. So clearly you need at least 8 colours.
You could go ahead and find an 8-colouring, but for an a more satisfying proof that 8 colours is sufficient:
Start with a 2x2x2 cube where all smaller cubes are distinctly coloured. Use the following algorithm:
1) Split your entire shape in half.
2) Fix one half, and reflect the other half about the fixed half. For example, this is what it would look like for a 2x2 square:
blue green
red yellow
Step 1) Fix the RHS half, so green and yellow are fixed.
Step 2) Reflect the LHS over the RHS:
blue green blue
red yellow red
As you can see, this process allows us to colour more cubes without the need for extra colours. This works because the line we are reflecting about will always separate cubes of the same colour (in this case the fixed green/yellow is separating the blue's and red's).
So starting with your 2x2x2 cube, we can do this process to obtain a 3x3x3 cube with only 8 colours, as so:
2x2x2 ---> 2x2x3 ---> 2x3x3 --->3x3x3 (try visualise this process)
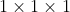 . Each cube is a single colour. Kangaroo want to use 27 small cubes to make a cube
. Each cube is a single colour. Kangaroo want to use 27 small cubes to make a cube 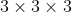 so that any two cubes with at least one common vertex are of different colours. At least how many colours have to be used?
so that any two cubes with at least one common vertex are of different colours. At least how many colours have to be used?

