-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Discrete random variables (2 Viewers)
- Thread starter leehuan
- Start date
Trying to calculate the variance of the uniform distribution and I don't know what the trick is to simplify the horrible looking sum
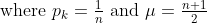
https://en.wikipedia.org/wiki/Faulhaber's_formula .)
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Yep, I basically forgot Var[X] = E[X2]-mu2. But thanks anyway
The Bernoulli distribution is the binomial distribution with n = 1. In fact, a Bin(n,p) random variable is just a sum of n i.i.d. (independent and identically distributed) Bern(p) (Bernoulli with parameter p) random variables.Question out of interest
Just like how you can call the Poisson distribution a limit of the binomial distribution, would you be able to say that the geometric distribution is just the binomial distribution for n=1
The geometric distribution can be considered a special case of the negative binomial distribution with r = 1 (or r = something else, depending on what convention is used).
Negative binomial distribution: https://en.wikipedia.org/wiki/Negative_binomial_distribution.
Last edited:
What you are calculating is the probability that X ≤ alpha, but we need the probability that the proportion is less than or equal to alpha (whereas X is the number).Ahh right
______________________
I'm doing something wrong.
(Ignore the alpha^2 bit for now)
 = \sum_{k=1}^\alpha{P(X=k)} \\ =\frac{2}{(n+1)(n+2)} \sum_{k=1}^{\alpha}{(k+1)}\\ =\frac{\alpha^2+3\alpha+2}{n^2+3n+2}$ is seemingly wrong$)
I think a Moderator moved it a while back. It is now here: http://community.boredofstudies.org/1003/maths/350202/university-statistics-discussion-marathon.html .Hey, whatever happened to the statistics marathon thing?
Basically the classic HSC greatest coefficient but I've forgotten how to do simple arithmetic tonight.
\\ $and I forgot how to use that to my advantage$)
Last edited:
It's always the mode.
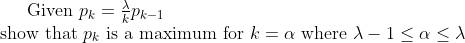
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Oops. Lol I feel dumb I was even thinking about how to manipulate p_k/p_k-1 Ok thanks again
Here's some hintsNever made a thread for approximations so I'll throw this question in this thread...

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
I don't believe it matters whether you have a discrete or continuous random variable so I'm randomly chucking it in this thread, but can I please have a proper example on what statistical independence is?
Like I get that Pr(A∩B) = Pr(A)Pr(B) for statistical independence but I kinda roted it, and don't fully understand it.
Which is why whilst I somewhat get this, I don't fully get it:

^2 \right] &=\mathbb E \left[ X^2 + 2XY + Y^2 \right] \\ &= \mathbb E \left[X^2 \right] + \mathbb E \left[2XY \right] + \mathbb E \left[Y^2 \right] \\ &= \mathbb E \left[X^2 \right] + \underbrace{2\mathbb E \left[X \right]\mathbb E \left[Y\right]}_{\text{given statistical independence}} + \mathbb E \left[Y^2 \right] \end{align*})
Also can I have a brief refresher on why expectation is linear again? Can I just argue that because summation/integration is linear?
Like I get that Pr(A∩B) = Pr(A)Pr(B) for statistical independence but I kinda roted it, and don't fully understand it.
Which is why whilst I somewhat get this, I don't fully get it:
Also can I have a brief refresher on why expectation is linear again? Can I just argue that because summation/integration is linear?
I don't believe it matters whether you have a discrete or continuous random variable so I'm randomly chucking it in this thread, but can I please have a proper example on what statistical independence is?
Like I get that Pr(A∩B) = Pr(A)Pr(B) for statistical independence but I kinda roted it, and don't fully understand it.
Which is why whilst I somewhat get this, I don't fully get it:
Also can I have a brief refresher on why expectation is linear again? Can I just argue that because summation/integration is linear?
https://proofwiki.org/wiki/Condition_for_Independence_from_Product_of_Expectations
.
https://proofwiki.org/wiki/Linearity_of_Expectation_Function
.
http://math.stackexchange.com/quest...r-under-what-conditions-is-median-also-a-line .
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Is there some way that conditional probability is supposed to work with random variables?
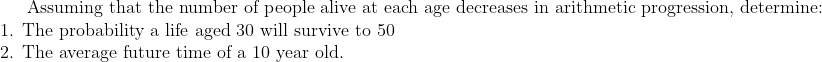
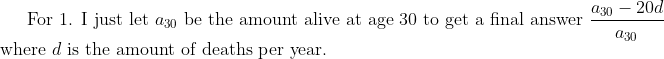
, so I started doing something like this:}\\ \text{Let }d=\text{deaths and }a=\text{initial.} \\ \begin{align*} Pr(X >10 | X=10) &= \frac{ P r( (X > 10) \cap (X=10) )}{ P r (X=10)}\\ &= \frac{ P r(?) }{\frac{a-10d}{a}} \end{align*})
And then I got lost.
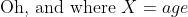
Possibly useful: My textbook (Pg 3 & Pg 14) had an example where instead they used expectation. But they actually started counting at age 0, and I have to start counting at age 10 so I wasn't sure how to use expectation here.
And then I got lost.
Possibly useful: My textbook (Pg 3 & Pg 14) had an example where instead they used expectation. But they actually started counting at age 0, and I have to start counting at age 10 so I wasn't sure how to use expectation here.
Last edited:
I think you would need to make an assumption about what the oldest possible age is, e.g. 100 years (or call it N years or something), because that'd clearly affect the answer.Is there some way that conditional probability is supposed to work with random variables?
And then I got lost.
Possibly useful: My textbook (Pg 3 & Pg 14) had an example where instead they used expectation. But they actually started counting at age 0, and I have to start counting at age 10 so I wasn't sure how to use expectation here.
Also, Pr(X > 10 | X = 10) is 0, so I think you meant something else.

