Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Vat... How does this even work ?
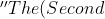 Principle of Mathematical Induction. $ \\ $ If, for any statement involving a positive integer, n, the following are true: $ \\ \\ $ The statement holds for n=1, and $ \\ \\ $ Whenever the statement holds for all n $ \geq k $, it must also hold for n=k+1 $ $ then the statement holds for all positive integers, n.'' $ )
Also how would we even use this...
Also how would we even use this...
It's not saying it holds for n>=k its just saying that n>=k.I was going to suggest strong induction but then I realised n≥k
But if it holds for all n≥k then technically must it hold for n=k+1 anyway?
It's not saying it holds for n>=k its just saying that n>=k.
You lost me. Looks like a redundancy
See if you can understand (or even agree) with the following statement regarding strong induction:(with correction)
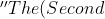 Principle of Mathematical Induction. $ \\ $ If, for any statement involving a positive integer, n, the following are true: $ \\ \\ $ The statement holds for n=1, and $ \\ \\ $ Whenever the statement holds for all n $ \leq k $, it must also hold for n=k+1 $ $ then the statement holds for all positive integers, n.'' $ )
It was never in the syllabus and hence was never required in the exams.Speaking of induction in the HSC, it is common for students to write a sort of mantra at the end of induction proofs in the HSC (or at least was common before, not sure if it still is). Basically an explanation of why induction works or something iirc. I think such a mantra is no longer needed in the HSC, so why is it / was it common for students to do? Was it once required in the HSC?

