You can use
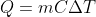
ONLY for the case when heat is transferred over convection or conduction. However you also have to take into account the thermal equilibrium of the whole system, including the environment (if there is no wind, then you can take final temperature as ambient air temperature of the room).
You can look at this two ways. I will explain both below.
For the case where the conductor is cooler than the ambient temperature: The value you get for Q is the amount of heat energy required to heat up the conductor to the ambient temperature (if necessary). m is the mass of the conductor, C is specific heat of the conductor and delta T is the change in temperature required for the conductor and room to reach thermal equilibrium. As long as the current isn't too high as so that the conductor is beginning to burn, the conductor will stay at this ambient temperature as the room will act as a heat dissipator.
For the case where the conductor is at a higher temperature than the ambient temperature: The value you get for Q is the amount of heat energy required to heat up the room to the temperature of the conductor. m is the mass of the gas/liquid/solid (remember, this is only for convection or conduction heat transfer!) within the proximity of the wire (ie the environment), C is the specific heat of the gas/liquid/solid and delta T is the change in temperature required for the environment and conductor to reach thermal equilibrium. In this case, the room will increase in temperature until the equilibrium is established. Effectively, for this whole process the room will again act as a heat dissipator.
For both of these conditions, the following will occur after equilibrium.
There is more electrical energy converted into heat energy in this system after this stage. So you ask, what is happening to this energy?
The whole system will rise in temperature. The differences in temperature will depend on the heat transfer rate from the wire to the environment which is dependent on many more various factors.
Think of this case as the same thing as a CPU and CPU heat sink. Imagine the wire as the CPU, whilst the environment is analogous to the heat sink. The heat sink will rise in temperature until it reaches the same temperature as the CPU. Then, they will both steadily increase in temperature. What saves this system from burning you ask? The fan for dissipating heat into the air. Generally, a good fan will ensure that the heat sink is cooled very quickly. If not, when the CPU returns to a low load and is actually generating less heat, the heat sink will transfer heat back to the CPU meaning the fan on the heat sink is not doing it's proposed job and is very bad for the application. You can also apply this analogy to a radiator core which can be found on a CPU or car engine as well for liquid cooling.
You had the right idea for convection and conduction cases, but you didn't apply the theory properly.


