-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (1 Viewer)
- Thread starter leehuan
- Start date
Re: Extracurricular Integration Marathon

 \, dx &= 2 \int^\infty_0 \sin (x^2) \, dx\end{align*})

 \, dx &= \int^\infty_0 \frac{\sin u}{\sqrt{u}} \, du. \quad (*)\end{align*})
} \int^\infty_0 z^{a - 1} e^{-uz} \, dz.)
} \int^\infty_0 \frac{e^{-uz}}{\sqrt{z}} \, dz = \frac{1}{\sqrt{\pi}} \int^\infty_0 \frac{e^{-uz}}{\sqrt{z}} \, dz.)
 as a double integral we have$)
 \, dx &= \frac{1}{\sqrt{\pi}} \int^\infty_0 \int^\infty_0 \frac{e^{-uz}}{\sqrt{z}} \sin u \, dz \, du\\&= \frac{1}{\sqrt{\pi}} \int^\infty_0 \int^\infty_0 \frac{e^{-uz}}{\sqrt{z}} \sin u \, du \, dz,\end{align*})

 \, dx &= \frac{1}{\sqrt{\pi}} \int^\infty_0 \frac{dz}{\sqrt{z} (1 + z^2)}.\end{align*})
 \, dx = \frac{2}{\sqrt{\pi}} \int^\infty_0 \frac{dt}{1 + t^4}.)
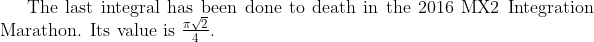
 \, dx = \frac{2}{\sqrt{\pi}} \cdot \frac{\pi \sqrt{2}}{4} = \sqrt{\frac{\pi}{2}}.)
For 4, I think people should still attempt it / try other methods, as it is much less clear why "letting a=-i" should be valid. Letting a=-1 would give us something nonsensical for example. Definitely need to say something more to justify the formula being the same as that of the Gaussian integral (and why that particular choice of square root and not the other).
Re: Extracurricular Integration Marathon

Here's a very deceptive integral which appears simple.
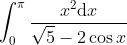
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon

Your nose does not deceive you.
Your nose does not deceive you.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
 , it's a bit lengthier than you can do it using complex analysis but I like the fact that a high school student could understand it.
, it's a bit lengthier than you can do it using complex analysis but I like the fact that a high school student could understand it.
Nice
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
}{(t-\frac{1}{t})^2+2} + \int \frac{\text{d}(t+\frac{1}{t})}{(t+\frac{1}{t})^2-2}=\frac{1}{\sqrt{2}}\tan^{-1}\left(\frac{t^2-1}{\sqrt{2}t}\right)+\frac{1}{2\sqrt{2}}\log\left(\frac{t^2 + \sqrt{2}t+1}{t^2-\sqrt{2}t+1}\right))
The good old tedious integral of 1/(1+t^4) haha.
Last edited:
Re: Extracurricular Integration Marathon
Ah right, I was thinking of the one with a t2 on the numerator too (the one that comes about when doing integral of √(tan x) ). That one was more tedious iirc. (Split into partial fractions etc.)
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon

No, that one is amenable to double symmetric substitution as well.Ah right, I was thinking of the one with a t2 on the numerator too (the one that comes about when doing integral of √(tan x) ). That one was more tedious iirc. (Split into partial fractions etc.)
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: Extracurricular Integration Marathon
=Re^{it}) for
for 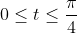
Then=Rie^{it})
So we have:
^2}Rie^{it}|dt =\int_0^{\frac{\pi}{4}} Re^{-R^2cos(2t)} dt \to 0 $~as~$ R \to \infty)

To make things neater we will define from now on=e^{-z^2})
We then integrate counter-clockwise about a boundary formed by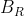 to make a circular arc and get:
to make a circular arc and get:
 dz - \int_0^R f(xe^{\frac{i \pi}{4}}) dx = 0)
Now take the limit as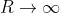
 dx = \frac{1+i}{\sqrt{2}} \int_0^{\infty} f(xe^{\frac{i \pi}{4}}) )
Now from a previously answered integral we know that:
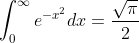
So we then have:
 = \frac{1+i}{\sqrt{2}} \int_0^{\infty} e^{-ix^2} dx)
Using Euler's formula we obtain:
+sin(x^2)+icos(x^2)-isin(x^2) dx)
Since the imaginary part = 0 we get:
 dx = \int_0^{\infty} sin(x^2) dx )
Now equating the real part gives:
 dx + \int_0^{\infty} sin(x^2) dx = \sqrt{\frac{\pi}{2}} )
 dx =\sqrt{\frac{\pi}{2}} )
 dx =\sqrt{\frac{\pi}{8}} )
Then we just double the answer cos even function to get:
 dx = \sqrt{\frac{\pi}{2}})
Let
Then
So we have:
To make things neater we will define from now on
We then integrate counter-clockwise about a boundary formed by
Now take the limit as
Now from a previously answered integral we know that:
So we then have:
Using Euler's formula we obtain:
Since the imaginary part = 0 we get:
Now equating the real part gives:
Then we just double the answer cos even function to get:
Last edited:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
}=4\pi\cot^{-1}{\sqrt{\phi}})
KingOfActing
lukewarm mess
Re: Extracurricular Integration Marathon
I've seen the solution to that integral before, good luck everyone.
3 substitutions and residue theorem
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Surely there must be more straightforward ways.
Is that the most straightforward way to do it?I've seen the solution to that integral before, good luck everyone.
Surely there must be more straightforward ways.
KingOfActing
lukewarm mess
Re: Extracurricular Integration Marathon

It's the way I've seen it done, there could be a simpler wayIs that the most straightforward way to do it?
Surely there must be more straightforward ways.
Re: Extracurricular Integration Marathon
 = \frac{1 - a \cos x}{1 - 2a \cos x + a^2}, \,\, |a| < 1.)
Here's a very deceptive integral which appears simple.
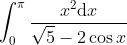
Re: Extracurricular Integration Marathon
 = \frac{1 - a \cos x}{1 - 2a \cos x + a^2}, \,\, |a| < 1.)
 \times \sum^\infty_{k = 0} a^k \cos (kx) &= \sum^\infty_{k = 0} a^k \cos (kx) - 2 \sum^\infty_{k = 0} a^{k + 1} \cos (kx) \cos x + \sum^\infty_{k = 0} a^{k + 2} \cos (kx)\\&= \sum^\infty_{k = 0} a^k \cos (kx) - 2 \sum^\infty_{k = 1} a^k \cos [(k - 1)x] \cos x + \sum^\infty_{k = 2} a^k \cos [(k - 2)x]\\&= 1 + a \cos x + \sum^\infty_{k = 2} a^k \cos (kx) - 2a \cos x - \sum^\infty_{k = 2} 2a^k \cos [(k - 1)x] \cos x + \sum^\infty_{k = 2} a^k \cos [(k - 2) x]\\&= 1 - a \cos x + \sum^\infty_{k = 2} a^k \left [\cos(kx) - 2 \cos [(k - 1)x] \cos x + \cos [(k - 2)x] \right ]\end{align*})
 + \cos (\alpha + \beta).\\$If we set $\alpha = (k - 1) x$ and $\beta = x$ we have$\\2 \cos [(k - 1)x] \cos x = \cos[(k - 2)x] + \cos (kx).)
 = \frac{1 - a \cos x}{1 - 2a \cos x + a^2},\\$as desired.)

 &= \frac{1 - a \cos x}{1 - 2a \cos x + a^2}\\1 + \sum^\infty_{k = 1} a^k \cos (kx) &= \frac{1 - a \cos x}{1 - 2a \cos x + a^2}\\2 + 2 \sum^\infty_{k = 1} a^k \cos (kx) &= \frac{2 - 2 \cos x}{1 - 2a \cos x + a^2}\\\Rightarrow 1 + 2 \sum^\infty_{k = 1} a^k \cos (kx) &= \frac{2 - 2a \cos x}{1 - 2a \cos x + a^2} - 1\\\Rightarrow 1 + 2 \sum^\infty_{k = 1} a^k \cos (kx) &= \frac{1 - a^2}{1 - 2a \cos x + a^2}\\\Rightarrow \frac{1}{1 - a^2} \left [1 + 2 \sum^\infty_{k = 1} a^k \cos (kx) \right ] &= \frac{1}{1 - 2a \cos x + a^2}\end{align*})

 \, dx\end{align*})

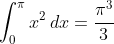

 \, dx &= \frac{2 \pi}{k^2} (-1)^k \quad \mbox{(using IBP twice)}\end{align*})
^k}{k^2} \right ].\end{align*})
$ is defined as $\mbox{Li}_s (x) \sum^\infty_{k = 1} \frac{x^k}{k^s}.)
^k}{k^2} = \mbox{Li}_2 (-a),$ a \textit{dilogarithmic} function. So finally we have)
 \right ] \quad (*)\end{align*})
\end{align*})
 can be rewritten as$\\\begin{align*}\int^\pi_0 \frac{x^2}{1 - 2a \cos x + a^2} dx = \frac{1}{1 + a^2} \int^\pi_0 \frac{x^2}{1 - \frac{2a}{1 + a^2} \cos x} dx \quad (***) \end{align*})
 with (***), we set $\frac{a}{1 + a^2} = \frac{1}{\sqrt{5}} \,\, \Rightarrow \,\, a^2 - a\sqrt{5} + 1 = 0.$ Thus $a = \frac{\sqrt{5} - 1}{2} = \frac{1}{\varphi},$ since $|a| < 1.$ Here $\varphi$ is the \textit{golden ratio}.)
 \right ].\end{align*})
 = -\frac{\pi^2}{15} + \frac{1}{2} \ln^2 \varphi.)
 = \frac{\pi^3}{15} + 2\pi \ln^2 \varphi.\end{align*})
Here's a very deceptive integral which appears simple.
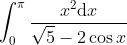
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
 .
.
One minor remark is that another way of proving the summation result used is taking the real part of the geometric series summation (common ratio z=a*cis(x)).
I.e. find the real part of 1/(1-a*cis(x)), which is quite quick.
Excellent solution to the integral
One minor remark is that another way of proving the summation result used is taking the real part of the geometric series summation (common ratio z=a*cis(x)).
I.e. find the real part of 1/(1-a*cis(x)), which is quite quick.
Re: Extracurricular Integration Marathon
Yes, I know, but I was trying to keep the problem "purely real" for the benefit of any MX2 students who may care to read this thread (though those who are reading this thread probably already know or could follow the complex way anyway).Excellent solution to the integral.
One minor remark is that another way of proving the summation result used is taking the real part of the geometric series summation (common ratio z=a*cis(x)).
I.e. find the real part of 1/(1-a*cis(x)), which is quite quick.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Anyway, nice answer. Here's the one I got from the place I found the problem.
 = \int_{-\pi}^{\pi} \frac{e^{iax}}{\sqrt{5}-2\cos{x}}$d$x\\$The integral we are after is $-\frac{1}{2}J''(0)=\int_0^\pi \frac{x^2}{\sqrt{5}-2\cos{x}}$d$x\\$Let us consider the following contour integral over $\mathbb{C}.\\ \oint_{C} \frac{z^a}{z^2 -\sqrt{5}z+1}$ where $C$ is a unit keyhole circle on the negative real axis.$\\$By the residue theorem, this is equal to $-2i\pi\phi^a\\$But this integral is also equal to $-iJ(a)+2i\sin{\pi a}\int_0^1 \frac{x^a}{x^2 +\sqrt{5}x+1} \\ $The section about the center of the circle vanishes, leaving us with $\\ J(a) = 2\pi \phi^a +2\sin{\pi a}\int_0^1 \frac{x^a}{x^2+\sqrt{5}x+1}$d$x \\$With a little computation, we have $-\frac{1}{2}J''(0) = -\pi\log^2{\phi}-2\pi\int_0^1 \frac{\log{x}}{x^2+\sqrt{5}x+1}$d$x \\$Using the facts:$\\ \frac{1}{x^2 + \sqrt{5}x+1} \equiv \frac{1}{x+\phi} - \frac{1}{x+\frac{1}{\phi}}\; ; \; \int_0^1 \frac{\log{x}}{x+a}$d$x = $ Li$_2\left(-\frac{1}{a}\right))
 = -\frac{\pi^2}{10}-\log^2 \phi \; ; \; $Li$_2(-\phi) = -\frac{\pi^2}{15}+\frac{1}{2}\log^2 \phi\\$We conclude $-\frac{1}{2}J''(0) = -\pi\log^2 \phi -2\pi\left[\left( -\frac{\pi^2}{10}-\log^2 \phi \right)-\left(-\frac{\pi^2}{15}+\frac{1}{2}\log^2 \phi \right)\right]\\$Hence $\int_0^\pi \frac{x^2}{\sqrt{5}-2\cos{x}}$d$x=2\pi\log^2 \phi+\frac{\pi^3}{15})
Don't bother, anyone who can follow this thread on the real analysis side probably has what it takes to follow the complex analysis side.Yes, I know, but I was trying to keep the problem "purely real" for the benefit of any MX2 students who may care to read this thread (though those who are reading this thread probably already know or could follow the complex way anyway).
Anyway, nice answer. Here's the one I got from the place I found the problem.

