I'm not good at explaining proofs but imagine a case like this for 2nd order DEs:
 \ \ \ ,$ P is some arbitrary function of $x. )
Where f is some function.
Now with a differential equation, imagine we have f as a function of x in terms of exponentials, say
 = G e^{k x} \ , \ \ $\ G, \ k \in \mathbb{R} )
What happens if we differentiate this? Well,
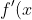 = Gk e^{kx} )
and
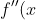 = Gk^2 e^{kx} )
So as you can see here, if we let the equation above at the top (but letting equal to zero), then we can obtain the homogeneous solutions to,

so as you can see by substituting these in, we get

What do we have here? A quadratic! Use the quadratic formula.
You will obtain two solutions at max (quadratic).
These solutions provide the necessary values of k as required.
Now, what we notice is that these values provide a solution in terms of the coefficients. However, if we had more than one solution, then we need to take into account both solutions. Say we get values
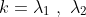
. These are just solutions to the quadratic.
So what we have here is the roots to a random quadratic. But really, what is the quadratic we speak of?
One way to think of it is:
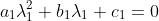
and

So,

So we have to take into account both of these. Do note however that here the coefficients of the quadratics could be anything as they are just constants. When taking this back to the function f, the constants can have any arbitrary value.
Hence to obtain the answer to f we have,
 = R e^{\lambda _1} + Q e^{\lambda _2} + U P(x)\ \ , R , \ Q, \ U \in \mathbb{C} )
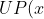 )
is for the particular solution by the way.
EDIT: You can find the values for R, Q and U by just using initial conditions for the f. For example, if f(0) = 0 and if f'(0) = 2, f''(0) = 1, then you can find these coefficients.
If there is a multiple root where
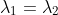
, there is a special case where we have something else.
A much better explanation than what I have above can be found in Paul's online notes if you can find it. For the multiple root case, consult this:
http://tutorial.math.lamar.edu/Classes/DE/RepeatedRoots.aspx
Say something if this doesn't make sense. I'm not all that great with explaining this type of stuff because I just usually find answers and put in the equation.

