For the questions:
c. Given y = 2xe^(2x)
i) Find dy/dx 2
ii) Hence evaluate int 4 xe^(2x).dx 3
(give your answer in exact form)
in ii), the answers go as the following:
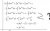
I can follow until the lines indicated by the question mark. I don't understand how the answer got from int 2e^(2x) to e^(2x) (right hand side on transition from 4line to 5th line)
In my answer, I did int 23^(2x) + int 4xe^(2x) = 2xe^(2x) + c
= 4e ^(2x) +D + int 4xe^(2x) = 2xe^(2x)+C
2
Int 4xe^(2x) =2xe^(2x) - 4e^(2x)
0
= [2xe^(2x) - 4e^(2x) ] with limits 2 and 0
= 4e^4 - 4e^4 -0-4e^0
= -4
c. Given y = 2xe^(2x)
i) Find dy/dx 2
ii) Hence evaluate int 4 xe^(2x).dx 3
(give your answer in exact form)
in ii), the answers go as the following:
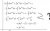
I can follow until the lines indicated by the question mark. I don't understand how the answer got from int 2e^(2x) to e^(2x) (right hand side on transition from 4line to 5th line)
In my answer, I did int 23^(2x) + int 4xe^(2x) = 2xe^(2x) + c
= 4e ^(2x) +D + int 4xe^(2x) = 2xe^(2x)+C
2
Int 4xe^(2x) =2xe^(2x) - 4e^(2x)
0
= [2xe^(2x) - 4e^(2x) ] with limits 2 and 0
= 4e^4 - 4e^4 -0-4e^0
= -4
