Escape velocity is the velocity
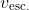
given by
=0\Leftrightarrow v_\text{esc.}=\sqrt{\frac{2GM}{R_\text{planet}}})
, where
M is the mass of the planet, and
Rplanet is the radius of the planet. Thus as you can see, the square root of the gravitational constant helps determine
vesc., and
vesc. is proportional to the square root of the mass of the planet, and inversely proportional to the square root of the planet's radius.
Here is the explanation why (i.e. how we derived the formula for
vesc.).
We are assuming there's no loss of energy from the spacecraft due to air resistance or other frictional effects etc. Therefore, the total mechanical energy (which is
Etot. = Ek + Ep) of the craft is conserved throughout its flight (conservation of energy). This means the value of
Etot. = Ek + Ep is constant at any point in time of the craft's flight. As we are launching it at escape velocity, we want in the limit at time goes to infinity, the distance the craft is from the planet to tend to infinity (this is the definition of the escape velocity: the craft will get arbitrarily far away from the planet as time goes on and on – it doesn't reach a maximum distance and then fall back down to Earth), and in this limit, the speed of the spacecraft will tend to 0. This means in the limit as
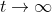
, we have
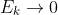
(because the velocity is tending to 0 as the earth's gravity keeps slowing the craft down) and
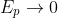
(because the distance
r of the craft tends to infinity, and as
r is in the denominator of the
Ep formula,
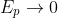
). This means the sum of kinetic energy and potential energy (i.e. total mechanical energy), in the limit as
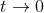
, is 0.
Since
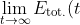=0)
, and we said earlier that by conservation of energy,
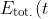)
is constant, it means this constant value is 0, i.e.
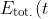=0$ $\forall t\geq0)
.
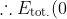=0\Rightarrow\frac{1}{2}mv_\text{esc.}^2+\left ( -\frac{GmM}{R_\text{planet}} \right )=0)
, since when time = 0, the craft starts at the planet's surface (hence
Ep has
Rplanet in the denominator, as this is the initial distance from the planet's centre), and the velocity is the escape velocity (since we're launching it at escape velocity), so
Ek initially equals
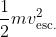
(
m is the mass of the craft).
So that's the explanation of how we got the equation at the start, from which we derived escape velocity's formula.

