Lol, I still don't get it, Integrand, can you please post steps on how to do this sort of question?
Basically, once you have that graph sketched, it's asking for the area underneath the
x-axis (i.e. area of the region bounded by the graph and the
x-axis from -½ to ½ ), PLUS the area under the curve from ½ to 1.
The area under the curve from -½ to ½ is found by finding
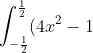\text{ d}x)
, and then taking the negative of this, since that integral is giving you a negative answer (integrating a function in a region where it is below the
x-axis gives negative of the area).
If you evaluate that integral (which I think you can do), you get -2/3. So taking the negative of that, you get +2/3. This is the area of the region below the
x-axis for that curve (i.e. from
x = -½ to ½).
Now evaluate the integral of the function from x = ½ to 1 to find the area of the region that's above the
x-axis (this integral is positive since the function is above the
x-axis in this region, so you don't need to worry about flipping the sign).
Evaluating it, you'll see it's 2/3. So the area of the part of the curve above the
x-axis is 2/3.
So the total area from -½ to 1 is:
(area of part under the
x-axis) + (area of part above the
x-axis) = 2/3 + 2/3 = 4/3.
