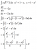-
Interested in being a marker for this year's BoS Maths Trials? Let us know before 31 August, see this thread for details
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX1 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Re: HSC 2015 3U Marathon
(I can see it easily for those values, but I haven't really considered values outside that range yet.)
Not sure, but does this question assume that 0 <= p <= 1 ?
(I can see it easily for those values, but I haven't really considered values outside that range yet.)
Re: HSC 2015 3U Marathon
In practice, p would be between 0 and 1, but the result seems to hold true for all other real p too.Not sure, but does this question assume that 0 <= p <= 1 ?
(I can see it easily for those values, but I haven't really considered values outside that range yet.)
Re: HSC 2015 3U Marathon
Just checking .... because it is a LONG LONG time since I've done this, but is this the expected value of a binomial distribution?In practice, p would be between 0 and 1, but the result seems to hold true for all other real p too.
Re: HSC 2015 3U Marathon

It is indeed.Just checking .... because it is a LONG LONG time since I've done this, but is this the expected value of a binomial distribution?
FrankXie
Active Member
Re: HSC 2015 3U Marathon
P.S. if you can prove it is true for 0<=p<=1, that actually means it is true for all real values of p. Because both LHS and RHS are polynomials of p of degree less than or equal to n, and if they are equal to each other at more than n points then they must be identical.
Just checking .... because it is a LONG LONG time since I've done this, but is this the expected value of a binomial distribution?
but only binomial expansion is needed to solve this problem. I've had one method in mind.It is indeed.
P.S. if you can prove it is true for 0<=p<=1, that actually means it is true for all real values of p. Because both LHS and RHS are polynomials of p of degree less than or equal to n, and if they are equal to each other at more than n points then they must be identical.
Last edited:
FrankXie
Active Member
Last edited:
Re: HSC 2015 3U Marathon
^n = \sum_{k=0}^{n}\binom{n}{k}x^k y^{n-k}) (by the binomial theorem)
(by the binomial theorem)
^n] = \frac{\partial }{\partial x}\left (\sum_{k=0}^{n}\binom{n}{k}x^k y^{n-k} \right ))
^{n-1}= \sum_{k=0}^{n}\frac{\partial }{\partial x}\binom{n}{k}x^k y^{n-k} ) (derivative of a sum is sum of derivatives on RHS)
(derivative of a sum is sum of derivatives on RHS)
^{n-1}= \sum_{k=0}^{n}k\binom{n}{k}x^{k-1} y^{n-k} ) .
.
Set and
and  , so x + y = 1, then
, so x + y = 1, then
^{n-k} ) .
.
Multiplying through by p yields^{n-k} ) (since
(since =\sum_{k=0}^{n}p\cdot f(k)) and
and  ) .
) . 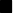
Nice. Here was my attempt:
Set
Multiplying through by p yields
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 3U Marathon

Attachments
-
56.8 KB Views: 96
Last edited:
FrankXie
Active Member
Re: HSC 2015 3U Marathon
NEXT QUESTION

NEXT QUESTION
Re: HSC 2015 3U Marathon
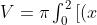(x-2)]^{2} \, \, dx $)
Is the answer found by working outNEXT QUESTION

FrankXie
Active Member
Re: HSC 2015 3U Marathon
incorrect. your calculation is true for the volume of solid generated by rotating that region about x axis, but not y axis.Is the answer found by working out
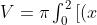(x-2)]^{2} \, \, dx $)
Re: HSC 2015 3U Marathon
 \\ y=-[(x-1^{2}-1)] \,\,\,\,\,($by completing the square$) \\ y=-(x-1)^{2}+1 \\ -y+1=(x-1)^{2}\\ 1\pm\sqrt{-y+1}=x \rightarrow\,\,\,\, $We will need both branches.$ \\\\\\ $Region A: (Using branch 1)$ \\ x=1-\sqrt{-y+1} \\ x^{2}= 2-2\sqrt{-y+1} -y \\ \therefore V=\pi\int_{0}^{1} (2-2\sqrt{-y+1} -y)\,\,dy \\ \\ \\ $Region B: (Using branch 2)$ \\x=1+\sqrt{-y+1}\\ x^{2}=2+2\sqrt{-y+1}-y \\ V=\pi\int_{0}^{1} (2+2\sqrt{-y+1}-y) \,\,\, dy \\\\\\ \therefore \,\,\,$Volume of solid formed can be found by Volume of Region B - Volume of Region A.$ \\$i.e:$ \,\,\,\,\, V= \pi\int_{0}^{1} (2+2\sqrt{-y+1}-y) \,\,\, dy - \pi\int_{0}^{1} (2-2\sqrt{-y+1} -y)\,\,dy)
Here is my attempt:incorrect. your calculation is true for the volume of solid generated by rotating that region about x axis, but not y axis.
FrankXie
Active Member
Re: HSC 2015 3U Marathon
NEXT QUESTION
+k(\cos\theta-2\sin\theta)|\leq1 $ is true for all real $ \theta ? )
NEXT QUESTION
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 3U Marathon
Working may be invalid, however GeoGebra does agree with my final answer.
http://i1164.photobucket.com/albums/q566/Rui_Tong/IMG_1522_zpsve7bxkqa.jpgNEXT QUESTION
+k(\cos\theta-2\sin\theta)|\leq1 $ is true for all real $ \theta ? )
Working may be invalid, however GeoGebra does agree with my final answer.
- Status
- Not open for further replies.