Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page

HSC 2014 MX2 Marathon ADVANCED (archive) (1 Viewer)

Thread starter Trebla
Start date Mar 19, 2014

Status: Not open for further replies.

Sy123

This too shall pass

#121

Re: HSC 2014 4U Marathon - Advanced Level

$\\ $For$ \ p_4(x) = \sum_{k=0}^4 \frac{x^k}{k!} \ \ \ \lim_{x \to -\infty} = \infty \ \ $and$ \ \ \lim_{x \to \infty} = \infty \\ \\ $Assume$ \ p_4 \ $has a root$ \ \alpha \\ $Either$ \ \alpha \ $is a double root, or if$ \ \alpha \ $is a root, there is at least one$ \ \beta \ $root with$ \ \alpha < \beta \\ $It is clear then that$ \ p'(\alpha) < 0 \ $and$ \ p'(\beta) > 0 \\ \\ $Now, $ \ \ p_4'(x) = p_4(x) - \frac{x^4}{24} \ \ \Rightarrow \ p_4'(\beta) = p(\beta) - \frac{\beta^4}{24} = -\frac{\beta^4}{24} < 0 \ \ \ $a contradiction!$ \\ \\ \therefore \ $There is no real root$ \ \alpha \ $hence$ \ p_4(x) > 0$

$\\ $Similar method as above, generalizing for$ \ \ p_{2n}'(x) = p_{2n}(x) - \frac{x^{2n}}{(2n)!}$

$\\ $If$ \ n \ $is odd, then$ \ p_{2k+1}'(x) = p_{2k}(x) \ $which has no roots, therefore$ \ p_{2k+1} \ $is monotone increasing, thus there can only be one real root, and since$ \ p(0) = 1 > 0 \ $then this root must be negative$$

J

juantheron

Active Member

#122

Re: HSC 2014 4U Marathon - Advanced Level

For (1) part::

$\\ $For$ \ p_4(x) = \sum_{k=0}^4 \frac{x^k}{k!} = 1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24} = \frac{1}{24}\left(x^4+4x^3+12x^2+24x+24\right)$

$Now\;\; \displaystyle \left(x^4+4x^3+12x^2+24x+24\right) = \left(x^4+4x^3+4x^2\right)+8\left(x^2+3x+\frac{9}{4}\right)+24-18$

$So\;\; \displaystyle \frac{1}{24}\left(x^4+4x^3+12x^2+24x+24\right) = \frac{1}{24}\lfet\{\left(x^2+2x\right)^2+8\left(x+1.5\right)^2+8\right\}>0\;\forall x\in \mathbb{R}$

Sy123

This too shall pass

#123

Re: HSC 2014 4U Marathon - Advanced Level

$\\ $Show for positive real$ \ a,b,c \\ \\ \frac{a^2}{(a+b)(a+c)} + \frac{b^2}{(b+c)(b+a)} + \frac{c^2}{(c+a)(c+b)} \geq \frac{3}{4}$

J

jyu

Member

#124

Re: HSC 2014 4U Marathon - Advanced Level

Sy123 said:
$\\ $Show for positive real$ \ a,b,c \\ \\ \frac{a^2}{(a+b)(a+c)} + \frac{b^2}{(b+c)(b+a)} + \frac{c^2}{(c+a)(c+b)} \geq \frac{3}{4}$

the inequality shows symmetry in a, b and c. nature does not favor one or the other.
minimum value when a=b=c=3/4

Sy123

This too shall pass

#125

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
the inequality shows symmetry in a, b and c. nature does not favor one or the other.
minimum value when a=b=c=3/4

Wait is this an actual theorem? What is it called?

seanieg89

Well-Known Member

#126

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
the inequality shows symmetry in a, b and c. nature does not favor one or the other.
minimum value when a=b=c=3/4

Symmetry in variables does not mean that minima occur when all variables are equal...

D

Davo_01

Active Member

#127

Re: HSC 2014 4U Marathon - Advanced Level

Sy123 said:
$\\ $Show for positive real$ \ a,b,c \\ \\ \frac{a^2}{(a+b)(a+c)} + \frac{b^2}{(b+c)(b+a)} + \frac{c^2}{(c+a)(c+b)} \geq \frac{3}{4}$

$ab(a+b)\geq 2ab\sqrt{ab}$

$\therefore ab(a+b)+ac(a+c)+bc(b+c) \geq 2(ab\sqrt{ab}+ac\sqrt{ac}+bc\sqrt{bc})$ $\geq 6abc$

$4(ab(a+b)+ac(a+c)+bc(b+c))$ $\geq 3(ab(a+b)+ac(a+c)+bc(b+c)+2abc)$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{ab(a+b)+c^2 (a+b)+ac(a+b)+bc(a+b)}\geq \dfrac{3}{4}$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{(a+b)(c^2+ab+ac+bc)}\geq \dfrac{3}{4}$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{(a+b)(a+c)(b+c)}\geq \dfrac{3}{4}$

$\dfrac{a^2}{(a+b)(a+c)} + \dfrac{b^2}{(b+c)(b+a)} + \dfrac{c^2}{(c+a)(c+b)} \geq \dfrac{3}{4}$

Last edited: Apr 19, 2014

J

jyu

Member

#128

Re: HSC 2014 4U Marathon - Advanced Level

seanieg89 said:
Symmetry in variables does not mean that minima occur when all variables are equal...

in this case when does minimum occur?

Sy123

This too shall pass

#129

Re: HSC 2014 4U Marathon - Advanced Level

Davo_01 said:
$ab(a+b)\geq 2ab\sqrt{ab}$

$\therefore ab(a+b)+ac(a+c)+bc(b+c) \geq 2(ab\sqrt{ab}+ac\sqrt{ac}+bc\sqrt{bc})$ $\geq 6abc$

$4(ab(a+b)+ac(a+c)+bc(b+c))$ $\geq 3(ab(a+b)+ac(a+c)+bc(b+c)+2abc)$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{ab(a+b)+c^2 (a+b)+ac(a+b)+bc(a+b)}\geq \dfrac{3}{4}$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{(a+b)(c^2+ab+ac+bc)}\geq \dfrac{3}{4}$

$\dfrac{a^2 (b+c)+b^2 (a+c)+c^2 (a+b)}{(a+b)(a+c)(b+c)}\geq \dfrac{3}{4}$

$\dfrac{a^2}{(a+b)(a+c)} + \dfrac{b^2}{(b+c)(b+a)} + \dfrac{c^2}{(c+a)(c+b)} \geq \dfrac{3}{4}$

Nice! Well done.

Here is my solution:

(Using cyclical sum notation to shorten writing)

$\\ \sum_{cyc} \frac{a^2}{(a+b)(a+c)} = \sum_{cyc} \frac{1}{\left(1 + \frac{b}{a} \right) \left(1 + \frac{c}{a} \right)} \\ x = \frac{b}{a} \ , \ y = \frac{c}{b} \ , \ z = \frac{a}{c} \ \Rightarrow \ xyz = 1 \\ = \sum_{cyc} \frac{1}{(1+x) \left(1+ \frac{1}{z}\right)} = \sum_{cyc} \frac{x}{(1+x)(1+y)} \\ = \frac{x(1+z) + y(1+x) + z(1+y)}{(1+x)(1+y)(1+z)} = \frac{(x+y+z) + (xy+xz+yz)}{1 + (x+y+z) + (xy+xz+yz) + xyz} \\ = \frac{(x+y+z) + (xy+xz + yz)}{2 + (x+y+z) + (xy+xz+xz)} = \frac{\alpha}{\alpha + 2} \\ $where$ \ \alpha = (x+y+z) + (xy+xz+yz) \\ f(\alpha) = \frac{\alpha}{\alpha + 2} \geq \frac{3}{4} \ \ $when$ \ \alpha \geq 6 \\ $Since$ \ x+y+z \geq 3\sqrt[3]{xyz} = 3 \ $and$ \ xy+xz+zy \geq 3\sqrt[3]{x^2y^2z^2} = 3 \\ \therefore \ \alpha \geq 6 \\ \therefore \ \frac{\alpha }{\alpha + 2} \geq \frac{3}{4} \\ \therefore \ \sum_{cyc} \frac{a^2}{(a+b)(a+c)} \geq \frac{3}{4}$

seanieg89

Well-Known Member

#130

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
in this case when does minimum occur?

In this question it happens to occur when x,y and z are equal. But this isn't because of symmetry, this is because Davo has shown it above (the only steps where inequality was introduced was the applications of AM-GM, whose equality conditions we understand well.) Writing what you did is not valid because there is no reason (that you have provided) why such an expression HAS to be minimised at x=y=z.

J

jyu

Member

#131

Re: HSC 2014 4U Marathon - Advanced Level

A triangle with side lengths a, b, c is inscribed in a circle of radius 1. Prove that a+b+c>=abc.

J

jyu

Member

#132

Re: HSC 2014 4U Marathon - Advanced Level

seanieg89 said:
In this question it happens to occur when x,y and z are equal. But this isn't because of symmetry, this is because Davo has shown it above (the only steps where inequality was introduced was the applications of AM-GM, whose equality conditions we understand well.) Writing what you did is not valid because there is no reason (that you have provided) why such an expression HAS to be minimised at x=y=z.

In this case the minimum 3/4 is given. The expression equals the min value when a=b=c, this is chosen due to symmetry, or should I say the cyclic nature of the expression. If a, b and c are different then the expression will be >= 3/4.

seanieg89

Well-Known Member

#133

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
In this case the minimum 3/4 is given. The expression equals the min value when a=b=c, this is chosen due to symmetry, or should I say the cyclic nature of the expression. If a, b and c are different then the expression will be >= 3/4.

Yes, it does equal 3/4 when a=b=c. But this does not prove that this is a minimum, and you cannot assume 3/4 is a minimum because that is what the question is asking you to prove.

Symmetry means that a=b=c is often a good candidate for a minimum, but doesn't prove anything without additional information.

D

Davo_01

Active Member

#134

Re: HSC 2014 4U Marathon - Advanced Level

Sy123 said:
Nice! Well done.

Here is my solution:

(Using cyclical sum notation to shorten writing)

$\\ \sum_{cyc} \frac{a^2}{(a+b)(a+c)} = \sum_{cyc} \frac{1}{\left(1 + \frac{b}{a} \right) \left(1 + \frac{c}{a} \right)} \\ x = \frac{b}{a} \ , \ y = \frac{c}{b} \ , \ z = \frac{a}{c} \ \Rightarrow \ xyz = 1 \\ = \sum_{cyc} \frac{1}{(1+x) \left(1+ \frac{1}{z}\right)} = \sum_{cyc} \frac{x}{(1+x)(1+y)} \\ = \frac{x(1+z) + y(1+x) + z(1+y)}{(1+x)(1+y)(1+z)} = \frac{(x+y+z) + (xy+xz+yz)}{1 + (x+y+z) + (xy+xz+yz) + xyz} \\ = \frac{(x+y+z) + (xy+xz + yz)}{2 + (x+y+z) + (xy+xz+xz)} = \frac{\alpha}{\alpha + 2} \\ $where$ \ \alpha = (x+y+z) + (xy+xz+yz) \\ f(\alpha) = \frac{\alpha}{\alpha + 2} \geq \frac{3}{4} \ \ $when$ \ \alpha \geq 6 \\ $Since$ \ x+y+z \geq 3\sqrt[3]{xyz} = 3 \ $and$ \ xy+xz+zy \geq 3\sqrt[3]{x^2y^2z^2} = 3 \\ \therefore \ \alpha \geq 6 \\ \therefore \ \frac{\alpha }{\alpha + 2} \geq \frac{3}{4} \\ \therefore \ \sum_{cyc} \frac{a^2}{(a+b)(a+c)} \geq \frac{3}{4}$

Nice, very clever

seanieg89

Well-Known Member

#135

Re: HSC 2014 4U Marathon - Advanced Level

seanieg89 said:
Yes, it does equal 3/4 when a=b=c. But this does not prove that this is a minimum, and you cannot assume 3/4 is a minimum because that is what the question is asking you to prove.

Symmetry means that a=b=c is often a good candidate for a minimum, but doesn't prove anything without additional information.

Picture it this way in two variables x and y:

A real function f can be viewed as a graph z=f(x,y).

Saying such a function is symmetric, is just saying that it's graph has reflective symmetry about the plane x=y.

This just means that any extrema will have a "mirrored" extrema on the other side of this plane. It definitely does not imply that every extrema must lie on x=y.

J

jyu

Member

#136

Re: HSC 2014 4U Marathon - Advanced Level

Look at some easier examples to picture. Area of a rectangle of fixed perimeter = xy, symmetry in x and y; volume of a cuboid of fixed surface area = xyz, symmetry in x, y and z.

seanieg89

Well-Known Member

#137

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
Look at some easier examples to picture. Area of a rectangle of fixed perimeter = xy, symmetry in x and y; volume of a cuboid of fixed surface area = xyz, symmetry in x, y and z.

So what if some symmetric expressions have extrema when all variables are equal? This does not mean that all do, so we can't use it in proofs.

Here is a symmetric expression in two variables, (switching x and y just switches the roles of the two bracketed terms).

$$Let $P(x,y)=((x+1)^2+(y-1)^2)\cdot((x-1)^2+(y+1)^2)$

But P only attains it's minimum of 0 at (1,-1) and (-1,1). When x=y, it is positive.

Why does your "rule" apply for the question Sy asked, but not for the expression in this post?

Last edited: Apr 19, 2014

Sy123

This too shall pass

#138

Re: HSC 2014 4U Marathon - Advanced Level

jyu said:
A triangle with side lengths a, b, c is inscribed in a circle of radius 1. Prove that a+b+c>=abc.

Great question!

Minor corrections:

$f(x) = \sin x - \sin(2x) \ \ $is convex on$ \ x \in [0, \pi]$

J

jyu

Member

#139

Re: HSC 2014 4U Marathon - Advanced Level

seanieg89 said:
So what if some symmetric expressions have extrema when all variables are equal? This does not mean that all do, so we can't use it in proofs.

Here is a symmetric expression in two variables, (switching x and y just switches the roles of the two bracketed terms).

$$Let $P(x,y)=((x+1)^2+(y-1)^2)\cdot((x-1)^2+(y+1)^2)$

But P only attains it's minimum of 0 at (1,-1) and (-1,1). When x=y, it is positive.

Why does your "rule" apply for the question Sy asked, but not for the expression in this post?

Because of the constants.
Change x+1 to X and y-1 to Y,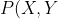 $P(X,Y)=(X^2+Y^2)\cdot((X-2)^2+(Y+2)^2)$

seanieg89

Well-Known Member

#140

Re: HSC 2014 4U Marathon - Advanced Level

The constants? Which constants and what about them?

What is the purpose of this coordinate change? P is not symmetric in X and Y (and we should not expect it to be, because the relationship between (x,y) and (X,Y) breaks symmetry.

Your claim was:

Symmetry in variables => Any minimum must happen when all variables are equal.

I provided an example of an expression that is (A) symmetric, and (B) does not have a minimal point with x=y, but has a minimum elsewhere.

If you think this is not a counterexample to your claim then you must contest one of these two assertions. Which one, and why? Please be precise, as I am making an effort to.

Status: Not open for further replies.

Share:

Facebook Twitter Reddit Pinterest Tumblr WhatsApp Email Link

Users Who Are Viewing This Thread (Users: 0, Guests: 1)

Top