you can either:
i) use the equation of tangent for an ellipse 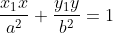
and then just sub in (6,-2) as x1 and y1, a=3 and b=2
or if that's unknown (or you don't know how to find it yet)
ii) implicitly differentiate the equation ( http://www.sosmath.com/calculus/diff/der05/der05.html ) - dy/dx will give you the gradient; sub the point (6,-2) in.
then just use point-gradient formula: y-y1=dy/dx(x-x1)
ii) is the method you use to find the result in i)
oops I read the question wrong. LOL
I suppose you can just find the chord of contact
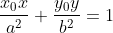
where (x0,y0) is (6,-2) and then find the point of intersection (make y the subject and sub the equation into the ellipse) and sub that into the tangent to ellipse equation. Here's what I came up with:
https://www.dropbox.com/s/5wfhk56i9klvmx0/Scan0004.jpg but hopefully someone has a shorter and smarter method haha.