-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012-14 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter bleakarcher
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Here is my attempt for the third one:
 = I = \int_0^{\pi} \ln (a^2- 2a\cos x +1) \ dx = \int_0^{\pi} \ln (a^2 - 2a\cos(\pi -x) + 1) \ dx \ \ \ \ $since$ \ \int_0^b f(x) \ dx = \int_0^b f(b-x) \ dx \\ \\ $Therefore$ \ 2f(a) = \int_0^{\pi} \ln((a^2-2a\cos x+1)(a^2+2a\cos x+1)) \ dx = \int_0^{\pi} \ln(a^4 -2a^2 \cos(2x) + 1) \\ \\ u= 2x \\ \\ \int_)^{2\pi} \frac{1}{2}\ln(a^4-2a^2\cos u +1) \ du \\ \\ $And$ \\ \\ \int_0^{\pi} \ln(b^2 - 2b\cos z +1) \ dz = \int_{\pi}^{2\pi} \ln(b^2 - 2b\cos z + 1) \ dz \\ \\ $Therefore$ \ \ \int_0^{2\pi} \ln(b^2- 2b\cos z +1) = 2\int_0^{\pi} \ln(b^2 -2b\cos z + 1) \ dx \\ \\ \therefore \ 2f(a) = \frac{1}{2} 2f(a^2) \\ \\ \therefore \ 2f(a) = f(a^2) \\ \\ $The only function that satisifes this is$ \ f(a) = \ln a \\ \\ \therefore \ \int_0^{\pi} \ln(1-2a\cos x + a^2) \ dx = \ln a )
Is that correct?
Here are some more from me as well:
The third one is a little different in flavour.
Here is my attempt for the third one:
Is that correct?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
The functional equation 2f(a)=f(a^2) is right, but your subsequent deduction isn't. You aren't far off though.Here is my attempt for the third one:
Is that correct?
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
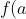 = \begin{cases} 0 , \ \ \ a=0 \\ \ln a, \ \ \ a > 0 \end{cases} )
?
Taking the seperate casesThe functional equation 2f(a)=f(a^2) is right, but your subsequent deduction isn't. You aren't far off though.
?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
This isn't the only solution to the functional equation (double it for instance and it's still a solution). More importantly though, this cannot be the correct value for the integral, because f(a) should tend to 0 as a->0.Taking the seperate cases
?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Are there more properties of the functions that need to be found?
Oh yes ok, how would you propose finding the constant k in the expression k ln(a)?This isn't the only solution to the functional equation (double it for instance and it's still a solution). More importantly though, this cannot be the correct value for the integral, because f(a) should tend to 0 as a->0.
Are there more properties of the functions that need to be found?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
The functional equation itself has many solutions, but by looking at what happens near zero we can make certain deductions about what f does in various places without having to explicitly find f. We can then use another identity coming from the initial integral definition of f to use this partial information to tell us what f does everywhere.
I never said that the solution was a multiple of log(a) for a > 0, I just said that any constant multiple of log(a) satisfies the functional equation.Oh yes ok, how would you propose finding the constant k in the expression k ln(a)?
Are there more properties of the functions that need to be found?
The functional equation itself has many solutions, but by looking at what happens near zero we can make certain deductions about what f does in various places without having to explicitly find f. We can then use another identity coming from the initial integral definition of f to use this partial information to tell us what f does everywhere.
darkness70
Member
Re: MX2 Integration Marathon
Prove they're equal?
Prove they're equal?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
I think a lot of the solutions to problems like this have a slightly different expression in different parts of the domain.
Just to be clear, when you ask for an indefinite integral like this, do you want people to post a function whose derivative is equal to the integrand on some part of the real line or do you want a function whose derivative is equal to your integrand everywhere on the real line?
I think a lot of the solutions to problems like this have a slightly different expression in different parts of the domain.
- Status
- Not open for further replies.




