HSC 2013 MX2 Marathon (archive) (2 Viewers)

[Sy123]

Re: HSC 2013 4U Marathon

 

[AnimeX]

Re: HSC 2013 4U Marathon

EDIT: On hindsight its actually very simple, 3141/1000 will do =(

==========

Which topic does this come under?

Can we use facts such as Area of circle, arc length etc?

 

[Sy123]

Re: HSC 2013 4U Marathon

Which topic does this come under?

Can we use facts such as Area of circle, arc length etc?

It may come under inequalities, the way I thought of doing it is considering area underneath 1/(1+x^2) and approximating through trapeziums.

Another way that comes to mind is proving the infinite series of pi/4 through integration of tan^{2n} x, then summing the first 20 terms or so by hand.

Area of circle or arc length might work, you just need to find a way of approximating both those through rational means, such as a area of an regular 20-gon or by considering multiple chords for arc length. Many ways are possible, but as I have said, the problem resolves into 3141/1000 :/

 

[braintic]

Re: HSC 2013 4U Marathon

EDIT: On hindsight its actually very simple, 3141/1000 will do =(

==========

355/113
It has an error of less than 10^-7
Justification: God's work???

 

[asianese]

Re: HSC 2013 4U Marathon

EDIT: On hindsight its actually very simple, 3141/1000 will do =(

==========

You can use a continued fraction algorithm.

 

[Sy123]

Re: HSC 2013 4U Marathon

Here is the question (fixed):

 

[Carrotsticks]

Re: HSC 2013 4U Marathon

It may come under inequalities, the way I thought of doing it is considering area underneath 1/(1+x^2) and approximating through trapeziums.

Another way that comes to mind is proving the infinite series of pi/4 through integration of tan^{2n} x, then summing the first 20 terms or so by hand.

Area of circle or arc length might work, you just need to find a way of approximating both those through rational means, such as a area of an regular 20-gon or by considering multiple chords for arc length. Many ways are possible, but as I have said, the problem resolves into 3141/1000 :/

But this is because you already know that pi=3.1415926.... (PS try memorising digits, pretty fun exercise).

What if you DIDN'T know this fact?

 

[Sy123]

Re: HSC 2013 4U Marathon

But this is because you already know that pi=3.1415926.... (PS try memorising digits, pretty fun exercise).

What if you DIDN'T know this fact?

Very true, so I can't know that my approximation is correct for an error of 10^{-3}? (which means that is a flaw in the question right?)
Or is there a way of showing that without knowing the digits of pi?

 

[Carrotsticks]

Re: HSC 2013 4U Marathon

Very true, so I can't know that my approximation is correct for an error of 10^{-3}? (which means that is a flaw in the question right?)
Or is there a way of showing that without knowing the digits of pi?

One could acquire an infinite series representation which somewhat represents a GP. Take the first couple of terms (say 4 or 5 terms of this series) and subtract it from the original infinite series. What you have remaining is an 'error term' which will still somewhat be in this 'GP form'. Play around with inequalities until a GP (with an existing limiting sum) is formed, and then acquire a closed form which will be easily comparable to 10^{-n}. An unfortunate consequence is that in the process of manipulating inequalities to force the limiting sum, you could have reduced say your initially 10^{-5} margin of error to 10^{-4}. So although you have a fairly sharp degree of accuracy, the process of determining this degree of accuracy makes it appear more 'blunt' than it actually is. Though, this is not necessarily a bad thing because it just means that you are sure that the approximation is correct to AT LEAST say 5 decimal places (when error term < 10^{-5} etc...). Motivation for this is that we have pi as an infinite series, so understandably its error term would also be an infinite series, but we want a closed form! So naturally limiting sum of GP comes to mind.

Another way would be to 'solve' the n'th term term of the infinite series. So for example, suppose the infinite series had the n'th term being 1/n^2 (I know this is wrong but just pretend), then you want 0 < 1/n < 10^{-4} for 4 decimal places, so solving this will yield n > 100 so the series will need at least 100 terms to be correct to 4 decimal places.

 

[Sy123]

Re: HSC 2013 4U Marathon

One could acquire an infinite series representation which somewhat represents a GP. Take the first couple of terms (say 4 or 5 terms of this series) and subtract it from the original infinite series. What you have remaining is an 'error term' which will still somewhat be in this 'GP form'. Play around with inequalities until a GP (with an existing limiting sum) is formed, and then acquire a closed form which will be easily comparable to 10^{-n}. An unfortunate consequence is that in the process of manipulating inequalities to force the limiting sum, you could have reduced say your initially 10^{-5} margin of error to 10^{-4}. So although you have a fairly sharp degree of accuracy, the process of determining this degree of accuracy makes it appear more 'blunt' than it actually is. Though, this is not necessarily a bad thing because it just means that you are sure that the approximation is correct to AT LEAST say 5 decimal places (when error term < 10^{-5} etc...). Motivation for this is that we have pi as an infinite series, so understandably its error term would also be an infinite series, but we want a closed form! So naturally limiting sum of GP comes to mind.

Another way would be to 'solve' the n'th term term of the infinite series. So for example, suppose the infinite series had the n'th term being 1/n^2 (I know this is wrong but just pretend), then you want 0 < 1/n < 10^{-4} for 4 decimal places, so solving this will yield n > 100 so the series will need at least 100 terms to be correct to 4 decimal places.

Yep I see what you mean. I'll give this a go tomorrow.

 

[seanieg89]

Re: HSC 2013 4U Marathon

Another way would be to 'solve' the n'th term term of the infinite series. So for example, suppose the infinite series had the n'th term being 1/n^2 (I know this is wrong but just pretend), then you want 0 < 1/n < 10^{-4} for 4 decimal places, so solving this will yield n > 100 so the series will need at least 100 terms to be correct to 4 decimal places.

Its important to note that this idea only works here because the series he is presumably working from (the arctan Maclaurin series evaluated at 1) is alternating. This generally would not be a valid way of bounding the error term of series.

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

From UNSW competition sample question:

A set of fifty pairwise distinct integers between 1 and 100 is chosen such that:

a) the sum of the numbers is equal to 2525; and
b) the sum of any two numbers never equals 101

Find the sum of squares of these integers.

 

[Sy123]

Re: HSC 2013 4U Marathon

From UNSW competition sample question:

A set of fifty pairwise distinct integers between 1 and 100 is chosen such that:

a) the sum of the numbers is equal to 2525; and
b) the sum of any two numbers never equals 101

Find the sum of squares of these integers.

Can you explain what hte question is saying in the first sentence? Is it saying that the integers from 1 to 100 are in pairs? Because if they're are then their sum would be 5050.

=======

In the x-y plane, there is an n*n grid of dots in the plane, all with integer co-ordinates

The triangle PQRis constructed on the grid of dots, such that all the points lie on a dot, the triangle is right angled at P, PQ is parallel to the y-axis and PR is parallel to the x-axis.

How many different triangles can be formed on the grid?

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

Can you explain what hte question is saying in the first sentence? Is it saying that the integers from 1 to 100 are in pairs? Because if they're are then their sum would be 5050.

Pairwise distinct integers just means that the integers are distinct with respect to one another I think. Simply put, you can not use an integer between 1 and 100 more than once.

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

Can you explain what hte question is saying in the first sentence? Is it saying that the integers from 1 to 100 are in pairs? Because if they're are then their sum would be 5050.

=======

In the x-y plane, there is an n*n grid of dots in the plane, all with integer co-ordinates

The triangle PQRis constructed on the grid of dots, such that all the points lie on a dot, the triangle is right angled at P, PQ is parallel to the y-axis and PR is parallel to the x-axis.

How many different triangles can be formed on the grid?

By different triangles, do you mean triangles with different co-ordinates as their vertices or triangles which are not congruent to each other, or they can be congruent if they are rotated?

 

[Sy123]

Re: HSC 2013 4U Marathon

By different triangles, do you mean triangles with different co-ordinates as their vertices or triangles which are not congruent to each other, or they can be congruent if they are rotated?

Different co-ordinates for at least 1 corner

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

Different co-ordinates for at least 1 corner

In that case I get

If this is right I'll post my solution.

edit: I just tried a different method and got

Not sure if either of these are right or why I get two different answers :/

 

[Sy123]

Re: HSC 2013 4U Marathon

In that case I get

If this is right I'll post my solution.

edit: I just tried a different method and got

Not sure if either of these are right or why I get two different answers :/

Yep nice work I get the first one, but using my method you get the factorised version first, n^2(n-1)(n-1) is that the same for yours?

EDIT: I don't know if its possible to get this but:

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

Yep nice work I get the first one, but using my method you get the factorised version first, n^2(n-1)(n-1) is that the same for yours?

Yep I get the factored version first.

 

[RealiseNothing]

Re: HSC 2013 4U Marathon

My solution is I can choose the point P in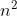 ways as it can take any point on the square. Then Q and R can both be chosen in (n-1) ways as they can take any point in the row or column that P was chosen in. Multiplying together gives the result.