Conics Question Help? (1 Viewer)

[namelyanonymous]

The question is (Question 9 from Fitz. 4 Unit 32(c)):

"P is a variable point on the ellipse with equation:



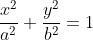
and S and S' are the focii. Show that PS and PS' are equally inclined to the tangent at P."

I have no idea what I'm trying to prove. What does it mean by "equally inclined"? If we're looking at perpendicular distance to the tangent, then isn't it obvious that they'd both have the same angle towards the tangent relative to the horizontal as they're both just points? Or am I looking at it the wrong way?

 

[HeroicPandas]

Let the points where tangent P cuts the x-axis and y-axis be X and Y respectively

Then i think it means u must try and prove that angle(SPX) = angle(S'PY)

 

[Sy123]

Let the points where tangent P cuts the x-axis and y-axis be X and Y respectively

Then i think it means u must try and prove that angle(SPX) = angle(S'PY)

Yep this is what it means.

It can be proven through repeated use of the angle between 2 lines formula, first find the gradient of the tangent at some P, then gradient PS, and PS'. Find the angle between PS and the tangent, and PS' and the tangent, if they are the same, then proof is complete.

Or, for a more geometrical proof, Choose to reflect the ellipse about the tangent. You will form a new ellipse with 2 new focii (say T and T'), where S reflected is T and S' reflected is T'.

Draw this out, and use it to prove that the angle S'PY = angle TPX. Which can be done by proving that S', P and T is collinear.
Then since angle TPX = angle SPX (reflection) therefore the proof is complete.

 

[namelyanonymous]

Thanks, guys! I'll try it out now.

Edit: Awesome got it! Thanks so much! And yep, I ended up using the angle-between-two-lines formula, ending up with:



The angle alpha is therefore the same size as beta, meaning that PS and PS' are equally inclined to the tangent.

 

[namelyanonymous]

I've got another question I need a bit of quick help with though. The question is:

P( p, 1/p) and Q (q, 1/q) are two varibale points on the rectangular hyperbola xy = 1.
a) If M is the midpoint of the chord PQ and OM is perpendicular to PQ, express q in terms of P

I found:

M = ((p+q)/2, (p+q)/2pq)
m(OM) = 1/pq
m(PQ) also turns out to be 1/pq

Since the gradients are equal, they're parallel not perpendicular. What am I doing wrong?

Thanks so much for the time!

Edit: Decided to make a new post http://community.boredofstudies.org/showthread.php?t=305396&p=6352387#post6352387 over here.