Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
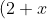^n = \binom{n}{0}+\binom{n}{1}(1+x) + \binom{n}{2} (1+x)^2 + \dots + \binom{n}{n}(1+x)^n )
Equate co-efficient of x^k
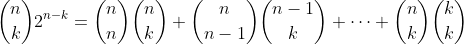
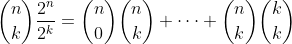
Express
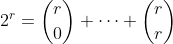
Sub it in, and we are done
Equate co-efficient of x^k
Express
Sub it in, and we are done



