Jashua_Long
Banned
- Joined
- Oct 15, 2012
- Messages
- 58
- Gender
- Undisclosed
- HSC
- N/A
Re: radians/degrees?=/
Q16 (b) was so easy. Just did it in less than 5 minutes.
Q16 (b) was so easy. Just did it in less than 5 minutes.
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
oh my frik, i was so close.. i had a bunch of cos, sin and tan crap but then I didn't know what to doThis is for 16b)
gradient OT = tan theta, therefore gradient tp = -1/tan theta...
point T is (sin theta, cos theta) and use equation of a line formula
yes you're correct sorry, typo. Definitely got it in the exam though!Point T is (cos theta, sin theta) or the other way around ?
Don't be surprised if you lose a mark.Hi! so i can do worked solutions if people want but basically here was how to do 16c i. took me a solid 30min to work out how to do it. Anyways.
equate the two graphs. so you get
y + (y-c)^2 = R^2.
y + y^2 - 2yc + c^2 - R^2 = 0
y^2 + y(1-2c) + (c^2 - R^2) = 0
now there are 2 equal and identical solutions to the above equation (because they intersect twice at the same location, just on oposite sides of the y axis)
hence the discriminate = 0
(1-2c)^2 - 4(c^2 - R^2) = 0 will then simplify down into the required answer, 4c = 1-4C^2
No idea how to do part ii though...
Q16 was easy, what u talking aboutThis. Working up to question 16 I was just like "make sure you don't make silly mistakes and should get a solid mark", nek minute hit Question 16, an hour later, fuck it I'll just check for silly mistakes. But if they hadn't of put in a fucked up question 16 then they would not have got a very good spread of marks imo.
Thats the newb way of finding the equation of the line.For those who still don't get part b), here is my solution that I used in the exam:
View attachment 26773
Sorry if there are some minor mistakes, I did this in like a couple of minutes.
Its the safest way to ensure you get the marks imoThats the newb way of finding the equation of the line.
How I got the equation of the line:
Gradient of OT is
Therefore gradient of TP is
T has co-ordinates
Therefore:
Then you just re-arrange to get:
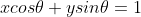
Don't be surprised if you lose a mark.
That is incorrect reasoning.
The graph has two intersection points. The correct reasoning is that the quartic equation should have a discriminant of zero to ensure two values of x.. If the quartic has zero discriminant, x^2 has only one solution. Therefore, x has two solutions.
They should penalise the people that did not include the reasoning (similiar to what I said above). I know tons of people would have just blindly set discriminant to zero (as the answer involved an equality, not a inequality) without actually thinking about what they were doing.
You can just as easily solve for 'y' and avoid any reasoning.I think they will penalise. It wasn't a question 16 for nothing. 1/2 without reasoning prolly.
shit...im an idiot.For those who still don't get part b), here is my solution that I used in the exam:
Q16 b).pdf
Sorry if there are some minor mistakes, I did this in like a couple of minutes.
Q16 was easy, what u talking about
Thats the newb way of finding the equation of the line.
Big deal mate. What are you trying to prove by coming on here and dissing everyone?Just looked at Q16 (a). So easy.
Easy similiarity proof with parallel lines and angles and then a simple ratio of corresponding sides.
Was a joke.
Done in 3 minutes.
