We need to powerful method of discussion here.
For the first one we have some sort of weird looking graph.
}{(x-2)(x+1)})
Now, from the graph you could notice a few things. One obvious thing is:
- As the function tends toward positive and negative infinity, it approaches the asymptote of -1.
This of course only can happen if g(x) takes a negative value AND if it holds the same degree as that of the denominator.
With this in mind the only possible answer is D.
[HR][/HR]
Now let's consider the second one.
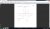
A) Well it's quite obvious that Q(w) is P(z) rotated anti-clockwise 90 degrees and halved in length. So of course A is correct.
B) Is incorrect. It is saying that the vector is rotated 90 degrees clockwise then truncated by half its length. Not true.
C) If we were to take the conjugate of w, it would be a reflect about the x axis. Clearly it cannot be rotated 90 degrees in any way to form the vector of z.
D)
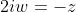
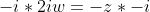

Same as first one! CORRECT!

[HR][/HR]
Next question.
Consider A, a is correct, because the conjugate is the reflection about the x axis. You may be thinking if might be some angle say 11pi/6 rads. However we are concerning the principle values. So adding them will result in zero. Hence A is correct.
Consider B, Clearly, the angle made with the positive real axis minus the argument made by z is 90!

Correct!
Consider C, NOPE! By observation!
Consider D, Correct. If we put some hypothetical values in, we always get -90!
[HR][/HR]
Next one. If we take the reciprocal function, it will always retain it's y value of 1 at the x coordinate. So the only possible answer is A.
Help me get off this website. It's ruining my HSC!