Re: 2012 HSC MX2 Marathon
I got two methods of doing it. I'm feeling quite tired right now, so I'll just outline the general idea. I might complete it some time later.
Method #1:
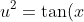)
... that the integral simplifies to

Then proceed to manipulate (which will involve dividing all terms by u^2 at some point), then use another substitution

And also:

Which will lead to the inverse tan integrals, in terms of K.
Method #2: (this one is a bit longer)
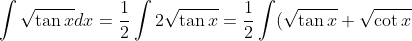 + (\sqrt{\tan x} - \sqrt{\cot x}) )
Split as two integrals, then turn all terms into sin and cos.
After a whole lot of manipulation, you will come across a situation where you will need the substitutions:

And similarly:

Then we will get a log standard integral and an inverse sine integral.
Oh and don't forget the +C (Spiral).


