-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Conics foci (1 Viewer)
- Thread starter Aysce
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
This is an ellipse that has been shifted to the left by 1 unit, and up 3 units.Q. {(x+1)^2}/8 + {(y-3)^2}/4 = 1 Find the foci and directrices. I dont understand how they got the foci.
We notice that this has the same focal length as the exact same ellipse, but centred at the origin.
So what I'll do is shift that ellipse back to the origin, find the foci, then shift the ellipse back to where it was originally (which will 'carry' the foci along with it).
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Here's some working out if you're having trouble:
 and (-2,0) $ \\\\ $We note that the new ellipse is the exact same one just then, but shifted to the left 1 unit, and up 3 units$. \\\\ $Hence, we will apply those transformations to the coordinates of the foci that we just found:$ \\\\ (2,0) \Rightarrow (1,3) \\\\ (-2,0) \Rightarrow (-3,3) )
Oh, and the directrices are found the same way. However this time, we need not shift it 'up' by 3 units, since the directrices are vertical lines anyway, so shifting them up or down will make no difference.
Oh, and the directrices are found the same way. However this time, we need not shift it 'up' by 3 units, since the directrices are vertical lines anyway, so shifting them up or down will make no difference.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Drawing a pretty diagram may help.
Our new centre of the ellipse was originally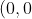,) now it's
now it's
)
For eccentricity,
)
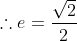
The coordinates of our ORIGINAL focii were)
=(\pm 2,0))
Since there was a shift of one units to the left, and three units up.
)
, (-3,3))
Our original directrices were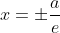
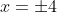
Shifting this left, since this only affects the abssicas not the ordinates.
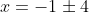
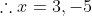
Our new centre of the ellipse was originally
For eccentricity,
The coordinates of our ORIGINAL focii were
Since there was a shift of one units to the left, and three units up.
Our original directrices were
Shifting this left, since this only affects the abssicas not the ordinates.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Spiral, you could have found the coordinates of the foci using the formula:
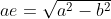
This automatically eliminates any need to find the eccentricity.
This automatically eliminates any need to find the eccentricity.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
The source Ace is using requires him to use the eccentricity method for practice.Spiral, you could have found the coordinates of the foci using the formula:
This automatically eliminates any need to find the eccentricity.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Not at all.Thank you guys, so much! Do you guys mind helping me with another question?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Let P be defined by the point (x,y), and define the point Q(2,1). Let the perpendicular distance between P and the line x+y-2=0 be l.<3
4b. Write the equation of the locus of a point P that moves such that its distance from (2,1) is half as its distance from the lie x+y-2=0.
This is a bit messy, but the equation should be a rotated ellipse.
You can leave it like this, or you can expand fully and add/subtract like terms etc.
