animeiswild
Member
- Joined
- Mar 6, 2011
- Messages
- 234
- Gender
- Female
- HSC
- 2012
Sorry forgot some brackets XD it's supposed to be sin(pi/n) not sin(pi)/nAre you sure that's right?
http://www.wolframalpha.com/input/?i=lim+n+approaches+infinity+nsin(pi)/n
It's from Yr 11 3u cambridge but could be 2u...
Sorry, are you referring to me? I am seriously asking a question here.That's L'Hopital's rule for indeterminate forms of limits. That's first year uni stuff.
Are you trolling?
No, it's not from the extension part, it's from the beginning of the development section.Is it from the "Extension" part of Cambridge exercises? Because that shit is ridiculous.
Sorry, I'm stupid. Please explain.lol this is actually just uses a result from the syllabus that
By letting, the result immediately follows
My question: are YOU trolling?That's L'Hopital's rule for indeterminate forms of limits. That's first year uni stuff.
Are you trolling?
This makes sense. Oh dear, my 3U is hazy.lol this is actually just uses a result from the syllabus that
By letting,
the result immediately follows noting that
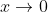
is equivalent to
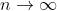
See the edited post.Sorry, I'm stupid. Please explain.
I saw. I could follow, then I lost it on the second last line. Where did the n at the beginning of sin go to?See the edited post.
Although L'Hopital's rule is indeed a useful tool most of the time, it doesn't necessarily mean that we must use it the moment we see a limit problemThat's L'Hopital's rule for indeterminate forms of limits. That's first year uni stuff.
Are you trolling?
