Question 8 (2 Viewers)

[Carrotsticks]

In case people haven't noticed, many Question 8's or Question 7's are either one of two things.


1. Elaborate and complicated proofs for very simple expresssions.
2. Proofs for the convergence of a particular series, and finding it's closed form.


For example...

2010 HSC

All of Question 8 was to prove that the Riemann Zeta function for s=2 converges to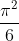 . Also known as the Basel Problem.

2009 HSC

Question 8 (b) and (c) was a proof utilising the Squeeze Law to prove that

Question 8 (a) was a proof for the convergence for a series (no latex, maybe later)

2008 HSC

Question 8 (b) was a proof for the fact that the surface area of a sphere is 4*pi*r^2

Question 6 (c) was a proof for the convergence for a series.

2007 HSC

Question 8 (c) was a proof for the fact that the limiting ratio between the perimeter and the average of the diagonals... is pi^2/2.

2006 HSC

Question 7 (c) was a proof for the limiting term of a sequence.

Question 8 (b) was a proof that the points of inflexion for the curve x^n*e^(-x) converge to share the same y value as n grows larger.

2005 HSC

Question 6 (a) was a proof for the series expansion for e.

2004 HSC

Question 8 (b) was a proof that a particular integral converges to 0 for large powers n.

2003 HSC

Question 8 (a) was a proof for a closed form of an open expression.

Question 8 (b) was a proof for the irrationality of pi by contradiction, which is reached by taking a limit.

2002 HSC

Question 8 (a) was the first half of the proof for the Riemann Zeta function for s=2. (Note: This was finally completed in 2010 HSC)

2001 HSC

Question 7 (a) was a proof for the closed form of an expression.

2000 HSC

Question 8 (a) was a proof for the closed form of an expression.

Hopefully you guys get the point. I may add in a bit of LaTeX later

The 2011 HSC was the only year not to have some sort proof for a limiting case. Although it is the most recent one (hence the best reflection of future HSC exams), I believe that students should still practise these questions to develop the skills necessary to confidently answer Question 8-type questions.

What I was hoping for, was to make a thread full of 'Question 8' type questions that students can practise on constantly, in preparation for school exams or even for the HSC.

These questions can be elaborate but elementary proofs for simple expressions that we take for granted such as:

- Area of a circle = pi*r^2
- Perimeter of a circle = 2*pi*r
- Volume of a sphere = 4/3 * pi*r^3
- Alternating Harmonic Series = ln(2)
- Leibniz's formula = pi/4 (EDIT: A preliminary approximation was deduced for this in 1997 HSC Q6 (a))
- Series expansions for e and pi (and perhaps other constants such as Euler's gamma constant)
- Riemann sum proofs for integrals

If you have any ideas, feel free to contribute.

Yes, I type these up myself, and yes I do use MathType for them.

Proof for convergence of Riemann Zeta function for s=2: http://www.mediafire.com/?1w857kfwotsog1d

Proof for that the area of a circle is pi*r^2: http://www.mediafire.com/?l2i4xoce2msjgpo

EDIT: I forgot that they are changing the format of the HSC. Consequently, the title should be Question 6. I'm guessing that the difficulty would be about the same.

 

[SpiralFlex]

There will not be any more question 8s when we do our HSC. They are cutting it down to 6 questions plus the objective response. But these proofs will still be useful for the last question.

I will see what I can find during the year.

Thank you for your hard work Sir Carrotsticks.

I highly suggest ALL Mathematics Extension 2 students read this!

 

[math man]

carrotsticks...do you remember the riemann sums question from this years adv integral calc test(MATH1903)....i think that would be a great question for these guys

 

[D94]

It is the complexity of the solution which compromises the simplicity of the concept. But really, the concepts mentioned such as Riemann Zeta, Squeeze Law, Leibniz's formula, or the series and geometric proofs mentioned, are never taught properly in class time. Even if you were taught the last 10 years worth of Q8, your year's Q8 could have no relation to any of the previous year's, and you need to be more than the up-to-Q7 capable student to answer Q8 correctly.

 

[Drongoski]

Very interesting & insightful analysis of Q8, Carrotsticks.

 

[Carrotsticks]

carrotsticks...do you remember the riemann sums question from this years adv integral calc test(MATH1903)....i think that would be a great question for these guys

Unfortunately, I do not remember it. However, there are some very nice questions from the tutorials that I can imagine appearing in an Extension 2 exam. Of course, they must be re-written (or sometimes simplified) such that it is doable for an Extension 2 student. These include proofs of the Wallis Product, and preliminary forms of Stirling's Approximation to the factorial.

It is the complexity of the solution which compromises the simplicity of the concept. But really, the concepts mentioned such as Riemann Zeta, Squeeze Law, Leibniz's formula, or the series and geometric proofs mentioned, are never taught properly in class time. Even if you were taught the last 10 years worth of Q8, your year's Q8 could have no relation to any of the previous year's, and you need to be more than the up-to-Q7 capable student to answer Q8 correctly.

I understand that the Q8 (or 6 lol) for 2012 could be TOTALLY different and have nothing to do with 2011 HSC, 2010 HSC etc. However, what I hope for students to gain from this, is the experience, and the exposure to the difficulty of such questions, so then they do not get overwhelmed in an exam.

Furthermore, the critical thinking skills and methods needed in these questions will most likely be required in future questions.

 

[math man]

the tute sheets are still up...so i will probs take them and tweak them a bit...o always planned to use some of them

 

[lolcakes52]

Very specifically, I remember an absolutely fantastic explanation of the formula or the area of a circle. It is here. I don't think that this will really benefit anyone in here but I think that the approach taken would benefit many people in their approach of any Q8. The website also has many great definitions and explanations of things such as e.

 

[Carrotsticks]

Very specifically, I remember an absolutely fantastic explanation of the formula or the area of a circle. It is here. I don't think that this will really benefit anyone in here but I think that the approach taken would benefit many people in their approach of any Q8. The website also has many great definitions and explanations of things such as e.

I have a proof for the area of a circle somewhere on my laptop. When I find it, I will post it. It utilises the Squeeze Law to prove that the area of a circle is pi*r^2.

 

[largarithmic]

On proving the area of a circle is pi*r^2 - the really nice and simple way I think is to prove the area of a sector with angle theta is 1/2 theta r^2, but that requires calculus I guess.

As for preparing for question 8 - I'm not *entirely* convinced that the best way to prepare for question eight is to do large numbers of analysis and/or summation questions. Frequently the infinite summation or square part of the question comes right at the end and is probably the "easiest" part: what I mean is, as long as the student has some understanding of some pretty intuitive concepts (like squeeze law) you can get the mark. The harder parts of q8 are usually applying knowledge and/or techniques in "non-standard ways" to actually get the inequalities and expressions which squeeze law is applied to.

In lieu of this I reckon the best way to prepare for q8 style things is generally... do hard and "non-standard" questions (e.g. extension questions from the textbooks, random stuff you can find, etc) to get used to applying knowledge sideways. Ultimately you'd probably learn more from this anyway, and be better prepared if the question (like in this year) was something completely unexpected.

On a particular source of questions, theres an exam in the UK called the STEP which is basically at the same level as q7-q8 HSC's. The questions are occasionally incredibly annoying and tedious but I think they're pretty decent and actually really accessible ways to get practice at "nonstandard" things.
http://www.admissionstests.cambridgeassessment.org.uk/adt/step/Test+Preparation
http://www.maths.cam.ac.uk/undergrad/admissions/step/advpcm.pdf

 

[Carrotsticks]

As for preparing for question 8 - I'm not *entirely* convinced that the best way to prepare for question eight is to do large numbers of analysis and/or summation questions. Frequently the infinite summation or square part of the question comes right at the end and is probably the "easiest" part: what I mean is, as long as the student has some understanding of some pretty intuitive concepts (like squeeze law) you can get the mark. The harder parts of q8 are usually applying knowledge and/or techniques in "non-standard ways" to actually get the inequalities and expressions which squeeze law is applied to.

Perhaps I should have been less ambiguous with this, if I was.

Doing limit questions at the very last part is very easy. Anybody knows how to take a limit. If you read the Marker's Comments for the last part of Question 8 in 2010 HSC, which required the application of a simple limit, they say that "many candidates wrote down the correct answer". Like you said, the hard part is to actually derive the expression to take the limit of. This is what I want people to practise.

However, when students do questions, surely they do not just do the part where they take the limit. They would of course attempt the entire question, which includes the actual derivation. I believe this pertains to your idea of applying knowledge or techniques in non-standard ways.

This is why I promote practising at this level of difficulty. When I was practising the 4U HSC, I did 30 HSC past papers from 1980 -> 2009. The exposure to difficult Integration by Parts questions, such as Question 8 of 2003 HSC, which required two applications of IBP, and the exposure to telescoping series (I forgot what year), allowed me to go through the 2010 Question 8 (which utilised Squeeze Law, 3 applications of IBP and telescoping sums).

I cannot guarantee that this will immediately mean 15/15 (or whatever the max mark is now), but I am quite sure that it will increase chances of obtaining marks due to prior-exposure.

 

[Shadowdude]

Squeeze Law? Come on, you know the cool kids use the "Pinching Theorem". Sounds better too.

 

[Carrotsticks]

Squeeze Law? Come on, you know the cool kids use the "Pinching Theorem". Sounds better too.

I actually wrote 'Sandwich Principle' in my MATH1907 assignment, and the marker circled it and wrote 'LOL'.

 

[Drongoski]

I learnt it as the "Sandwich Theorem".

 

[SpiralFlex]

My tutor says Sandwich Principle or Squeeze Theorem.

 

[largarithmic]

Perhaps I should have been less ambiguous with this, if I was.

Doing limit questions at the very last part is very easy. Anybody knows how to take a limit. If you read the Marker's Comments for the last part of Question 8 in 2010 HSC, which required the application of a simple limit, they say that "many candidates wrote down the correct answer". Like you said, the hard part is to actually derive the expression to take the limit of. This is what I want people to practise.

However, when students do questions, surely they do not just do the part where they take the limit. They would of course attempt the entire question, which includes the actual derivation. I believe this pertains to your idea of applying knowledge or techniques in non-standard ways.

This is why I promote practising at this level of difficulty. When I was practising the 4U HSC, I did 30 HSC past papers from 1980 -> 2009. The exposure to difficult Integration by Parts questions, such as Question 8 of 2003 HSC, which required two applications of IBP, and the exposure to telescoping series (I forgot what year), allowed me to go through the 2010 Question 8 (which utilised Squeeze Law, 3 applications of IBP and telescoping sums).

I cannot guarantee that this will immediately mean 15/15 (or whatever the max mark is now), but I am quite sure that it will increase chances of obtaining marks due to prior-exposure.

I guess the 'style' of questions acceptable for a q8 is actually kinda constant - they're sorta all in the category of analytical results that are slightly beyond the high school syllabus. I reckon the best way to prepare though would just be to... do harder stuff, because thats how neural pathways are made in your brain and you get better at maths. the exact type of question you're doing matters somewhat (obviously tending towards more analysis-syyyyy things might help) but any sort of hard question helps.

In terms of getting marks, I actually reckon drilling past papers is a pretty poor strategy unless you're sure you know everything already (in which case you should probably go study english or something) or unless you have a serious problem with exam technique. You wouldn't learn anywhere near as much from doing 20 polynomials questions spread out across 10 past papers over a fortnight than if you would doing 20 polynomials questions in one go, and maybe a few more the day after to consolidate stuff; then did complex numbers the next two days, etc.

 

[Carrotsticks]

I have added the proof for the area of a circle. Although easier than what would be in Question 8, it is still quite an elaborate proof.

The method used to prove it is called the Method of Exhaustion: http://en.wikipedia.org/wiki/Method_of_exhaustion

any sort of hard question helps.

Are Q8 questions not hard questions?

You wouldn't learn anywhere near as much from doing 20 polynomials questions spread out across 10 past papers over a fortnight than if you would doing 20 polynomials questions in one go

Think about it this way. Suppose I am training for a Triathlon (HSC), and I have a few days left. I have already done my primary training, and this is just a bit of final practice before the big event (although realistically you would have a tapering period). I want to familiarise myself with the conditions of the competition. I have two options:

1. 1 day swimming only, 1 day cycling only, 1 day running only.

2. 1 Triathlon per day for 3 days.

Which would you pick?

 

[largarithmic]

Are Q8 questions not hard questions?

You dont really see hard circle geometry q8 or hard counting q8. Theyre preeetty restrictive in the sort of difficulty they have, I reckon its worth looking at non-q 8 stuff

Think about it this way. Suppose I am training for a Triathlon (HSC), and I have a few days left. I have already done my primary training, and this is just a bit of final practice before the big event (although realistically you would have a tapering period). I want to familiarise myself with the conditions of the competition. I have two options:

1. 1 day swimming only, 1 day cycling only, 1 day running only.

2. 1 Triathlon per day for 3 days.

Which would you pick?

Depends how much time you have left and how well prepared you are. If its not only a week left though, I reckon theres still quite a bit of merit in doing questions in blocks - especially if youve noticed youre weaker in a particular area.

 

[seanieg89]

I learnt it as the "Sandwich Theorem".

I always found that name confusing because there is also a "Ham and Cheese Sandwich Theorem" in measure theory.

 

[Carrotsticks]

I reckon theres still quite a bit of merit in doing questions in blocks - especially if youve noticed youre weaker in a particular area.

I strongly agree.

This thread was aimed at people who want to get 95+ in Extension 2, so I did not take that into the equation, since students aiming for such marks tend to not have many 'weaker' areas.

I always found that name confusing because there is also a "Ham and Cheese Sandwich Theorem" in measure theory.

I did not know such a thing existed. I love these little quirky names for various theorems such as the 'Hairy Ball Theorem' in Algebraic Topology.