As mentioned above, integration is just the "opposite of differentiation".
The integral sign
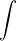
. Nice shape.
There are two types of integrals. Definite integrals and indefinite integrals.
For a start if we were asked to differentiate
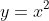
with respect to

, we would get
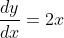
.
So if we were given the derivative, so how do we find integral of
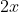
?
Indefinite integrals-
We will express in the form
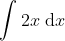
.
[Integrate
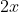
with respect to

]
Simply do via this process. Add a power, divide by new power.
If we add a power to
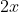
, we would get
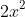
. Now divide it by that new power.

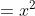
This is technically wrong however. We must add the constant of integration.

Why? This is because when we differentiate a constant it is gone, hence when we integrate it, we do not know what the constant is. Hence the constant of integration is used. This is by convention, "
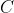
"

Simply attach an

if we are to integrate constants.
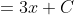
Now to the formal formula,

Example.
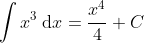
. Add a power and divide by that power.
Another formula,
^n \; \mathrm{d} x = \frac{(ax+b)^n^+^1}{a(n+1)})
Example.
If we were given a question like:
^7 \; \mathrm{d} x)
We could spend 1000 hours expanding this expression and then integrating piece by piece or we can use the formula above. It would be sensible and convenient to use the formula above.
^8}{3*8} +C)
^8}{24} +C) Definite integrals -
Definite integrals -
These types of integrations acquire a boundary of limit. Unlike indefinite integrals, these do not require the constant of integration.
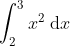
Simply integrate using our formulae as before. But do not put + C
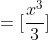
with limits 3 and 2.
Now here is what we do next. We substitute the value of 3 in. Then we substitute the value of 2 inside then you minus it.
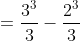
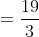
That is a summary of the basic concept of integration. Later on integration will be used to find area and volume. More integration techniques will be introduced such as integration by substitution.
____________________________________________________________
For your two unit course, you will need to learn how to integrate,
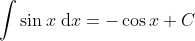
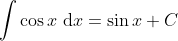



If you do three unit, the main ones are:
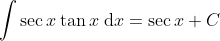

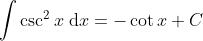
I haven't done 4U integration. Maybe another person can enlighten you on that.
_____________________________________________________________
Area
The positive area enclosed by a curve and the

axis.
We can now apply our integration techniques to find the area bounded by the curve and the

axis.
If we have a curve as such and we would like to find the area, we can do the following:
First I will introduce the area formula bounded by a curve and the

axis.
Area bounded by curve and

axis =
 \; \mathrm{d} x)
So applying this,
We can see that the boundaries of the area are 4 and 0.
 \; \mathrm{d} x)
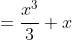
with limits 4, 0.
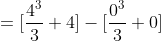
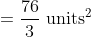
[
Note: If a negative area is present you treat it as a positive value by taking the absolute value of it.]
Compound areas
The graph shows the function of
=- x^3+ 6x)
We get two regions shaded in this. A positive region and a negative region.
Let us begin to integrate.
Area =
 WRONG!
WRONG!
You cannot simply integrate like this. Your negative region will cancel out your positive region if it is an even or odd function. Giving you an area of zero.
To integrate, I would advise you to always draw the curve.
We must use two integrals to find the area. But first we will find the

intercepts. Since our diagram has already done that, there is no need. We can begin integrating.
 \; \mathrm{d} x + \left |\int_{0}^{2} (-x^3+ 6x) \; \mathrm{d} x \right |)
TBC.
The positive area enclosed by a curve and the

axis.
Area bounded by curve and

axis =
 \; \mathrm{d} y)
I will edit this if you want me to continue.
Also I forgot my integrals to get inverse functions in my integral list.


