random-1005
Banned
- Joined
- Dec 15, 2008
- Messages
- 609
- Gender
- Male
- HSC
- 2009
lol, i made a mistake!!!, you we right first time with -33/56-20/63
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
lol, i made a mistake!!!, you we right first time with -33/56-20/63
LetA stone is thrown so that it will hit a bird at the top of a pole. However, the instant the stone is thrown, the bird flies away in a horizontal straight line at a speed of 10 metres per second. The stone reaches a height double that of the pole and, in its descent, (miraculously) touches the bird. Find the horizontal component of the velocity of the stone.
Theorm:Prove by induction that 9^(n+2) -4^(n) is divisable by 5 for all positive integers n .
oh right okayinverse ( to minus one), common notation on the net
NEW QUESTIONS:
1) Solve the equation4x^3+32x^2+79x+60=0 given that one root is equal to the sum of the other two.
2) Find the cubic equation whose roots are twice those of the equation 3x^2-2x^2+1=0
3) If two of the roots of the equation x^3+qx+r=0 are equal, show that 4q^3+27r^2=0
ps. dont forget to post a question once you've done one?
Letbe the initial horizontal velocity of the stone and let
be the initial vertical velocity of the stone.
Letbe the horizontal position of the pole with respect to the point of launch and
be the height of the pole. Let
be the
time it takes for the stone to reach the top of the pole andbe the time it takes to reach its maximum height.
Now because the parabola is symmetrical and so the stone is only at a vertical height ofat 2 times, namely
and
, so therefore the stone must hit the bird at
using all this...
We get 6 equations with 6 unknowns and we can solve for.
So basically your 6 equations are wrong, or not linearly independent.
You can easily check to see that this question has no unique solution.
Take W = 10,000m and and L = 1. Solve for U.
Take W = 1m and L = 1. Solve for U.)
Is that (n-r)/(r+1)?Question: Simplify nC(r+1) / (nCr)
Prove by induction that 9^(n+2) -4^(n) is divisable by 5 for all positive integers n .
hence by the process of MI... blah blah blah... proven true for all n
NEW QUESTION:
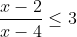
I think you may have forgotten to use this part of the questionYou are suggesting that their is a unique solution.
What does this mean?
This means if you can solve for a specific solution for U.
It means you can solve for a specific solution for L and W.
But we already know that L and W have no specific solution (in that they can be anything).
So basically your 6 equations are wrong, or not linearly independent.
You can easily check to see that this question has no unique solution.
Take W = 10,000m and and L = 1. Solve for U.
Take W = 1m and L = 1. Solve for U.

