-
Looking for HSC notes and resources? Check out our Notes & Resources page 
Another challenge question: Irrationality of e (1 Viewer)
- Thread starter seanieg89
- Start date
k02033
Member
so
clearly
factorizing gives
therefore
since
Now
where
therefore
as required
k02033
Member
Do we use proof by contradiction for the 2nd part?
Yeah, probs let e=p/q where p,q E Z+Do we use proof by contradiction for the 2nd part?
k02033
Member
dam stuck, will try again tomorrow
k02033
Member
1st thing i tried, didnt get anywhere >.>Yeah, probs let e=p/q where p,q E Z+
A bit late to be doing maths now? lol1st thing i tried, didnt get anywhere >.>
k02033
Member
more like forgot my discrete maths already, but yea i will run with the lame late excuse.A bit late to be doing maths now? lol
e-Sn=1/(n+1)!+...more like forgot my discrete maths already, but yea i will run with the lame late excuse.
So, 0<1/(n+2)!+...<1/(n(n+1)!)
Does the above help?
The proof is long-winded. It could've been proved a lot quicker if there was an "otherwise."
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Nice work with the inequality, and yes contradiction is pretty much the only way to go for the second part. Its not very long, just a little tricky.
Hint: Consider the proven inequality for certain special partial sums.
Hint: Consider the proven inequality for certain special partial sums.
Last edited:
k02033
Member
gurmies
Drover
That would be likely if it were |e-S_n| < ...Is e E (0,1/q) where e=p/q? And, this is a weird idea but is it legit to consider e as the magnitude of error between the bounds (ie. a distance)?
k02033
Member
ha ha the answer is funny, its so obvious
Theorem: e is irrational.
Proof by contradiction:
Let where p,q, are positive integers.
where p,q, are positive integers.
From part 1 we know
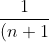!}< \frac{p}{q}-[1+1+\frac{1}{2!}+\frac{1}{3!}....\frac{1}{n!}]< \frac{1}{n\times n!})
Now let n=q and multiply throughout by q! gives
!-[2q!+1+\frac{q!}{2!}+\frac{q!}{3!}+...]<\frac{1}{q})
Now the middle term is an integer! And you cant have an integer satisfying that inequality therefore e is irrational, as required. I was way too stubborn with the gcd approach, 20 pages of trial and error ...
Theorem: e is irrational.
Proof by contradiction:
Let
From part 1 we know
Now let n=q and multiply throughout by q! gives
Now the middle term is an integer! And you cant have an integer satisfying that inequality therefore e is irrational, as required. I was way too stubborn with the gcd approach, 20 pages of trial and error ...
Last edited:
Fuck! I essentially had the last line but didn't deduce anything from it, so i chucked the paper in the binha ha the answer is funny, its so obvious
Theorem: e is irrational.
Proof by contradiction:
Letwhere p,q, are positive integers.
From part 1 we know
Now let n=q and multiply throughout by q! gives
Now the middle term is an integer! And you cant have an integer satisfying that inequality therefore e is irrational, as required. I was way too stubborn with the gcd approach, 20 pages of trial and error ...
k02033
Member
yay! i had it ages ago too, how embarrassing hahhaha ( i threw my pen couple of times)Fuck! I literally, had the last line but didn't deduce anything from it, so i chucked the paper in the binKudos, k02033. I would rep you again but need to spread the rep.
k02033
Member
Oh by the way, how do we put a space while using the latex equation editor?
Idk, i never use LaTeX. There's a LaTeX guide stickied somewhere in the Math forums.Oh by the way, how do we put a space while using the latex equation editor?
k02033
Member
Yeah, nw.
