MetroMattums
Member
- Joined
- Apr 29, 2009
- Messages
- 233
- Gender
- Male
- HSC
- 2010
Can anyone evaluate:
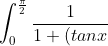^{k}} \,dx)
Thanks.
Thanks.
-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Integration Q (1 Viewer)
- Thread starter MetroMattums
- Start date
MetroMattums
Member
- Joined
- Apr 29, 2009
- Messages
- 233
- Gender
- Male
- HSC
- 2010
Many thanks.
Let u=pi/2-x: du=-dxCan anyone evaluate:
Thanks.
I=S [0,pi/2] dx/(1+(tan(x))^k)
= -S [pi/2,0] du/(1+(cot(u))^k)
= S [0,pi/2] (tan(u))^k du/((tan(u))^k+1)
= S [0,pi/2] 1-(1/((tan(u))^k+1) du
= S [0,pi/2] du -I
Thus, 2I=pi/2 => I=pi/4
Nice Q. Edit: Beaten
Brilliant as always. By the way, shouldn't the f(a-x)dx in line 1 read f(b-x)dx ?\,dx=\int_{0}^{b}f(a-x)\,dx $ which can be easily derived$\\\\\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+(\tan x)^k}\,dx\\\\=\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+(\tan (\frac{\pi}{2}-x))^k}\,dx\\\\=\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+\dfrac{1}{(\tan x)^k}}\,dx\\\\=\int_{0}^{\frac{\pi}{2}}\dfrac{(\tan x)^k}{1+(\tan x)^k}\,dx\\\\=\int_{0}^{\frac{\pi}{2}}\dfrac{1+(\tan x)^k-1}{1+(\tan x)^k}\,dx\\\\=\int_{0}^{\frac{\pi}{2}}\,dx-\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+(\tan x)^k}\,dx\\\\\Rightarrow 2\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+(\tan x)^k}\,dx=\int_{0}^{\frac{\pi}{2}}\,dx\\\\\therefore\int_{0}^{\frac{\pi}{2}}\dfrac{1}{1+(\tan x)^k}\,dx=\dfrac{\pi}{4})
Last edited:
That's a very minor error. In the worst case scenario you could just write 'let a=b'...