-
Interested in being a marker for this year's BoS Maths Trials? Let us know before 31 August, see this thread for details
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2 Unit Revising Marathon (1 Viewer)
- Thread starter jet
- Start date
blackratpoo
Member
- Joined
- Aug 22, 2008
- Messages
- 271
- Gender
- Female
- HSC
- 2010
Re: 2 Unit Revising Marathon HSC '10
how do you get that font? that wikipedia one that allows you to do (divide by signs)?
how do you get that font? that wikipedia one that allows you to do (divide by signs)?
Dragonmaster262
Unorthodox top student
Re: 2 Unit Revising Marathon HSC '10
a = -1 and b =1OK, now that 2010 is here I am reviving the old Revision Marathon game.
Rules:
The OP posts a question, first person to get it correct asks the next question, and so on.
First Question
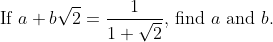
Dragonmaster262
Unorthodox top student
Re: 2 Unit Revising Marathon HSC '10
LaTeXhow do you get that font? that wikipedia one that allows you to do (divide by signs)?
gurmies
Drover
Re: 2 Unit Revising Marathon HSC '10
Please read the guidelines of this exercise, you must post a question upon answering one correctly (which you did).a = -1 and b =1
Dragonmaster262
Unorthodox top student
Re: 2 Unit Revising Marathon HSC '10
Sorry; my net got disconnected and it took ages to reconnect.
 = x^2/lnx )
Sorry; my net got disconnected and it took ages to reconnect.
Last edited by a moderator:
addikaye03
The A-Team
Re: 2 Unit Revising Marathon HSC '10
u'=2x, v'=1/x
y'=(vu'-uv')/v^2 (chain rule)
=[2xln(x)-x]/(lnx)^2
=x[2ln(x)-1]/(lnx)^2
Question; Solve: tanx=3cotx
u=x^2, v=ln(x)Sorry; my net got disconnected and it took ages to reconnect.
 = x^2/lnx )
u'=2x, v'=1/x
y'=(vu'-uv')/v^2 (chain rule)
=[2xln(x)-x]/(lnx)^2
=x[2ln(x)-1]/(lnx)^2
Question; Solve: tanx=3cotx
Last edited:
gurmies
Drover
Re: 2 Unit Revising Marathon HSC '10
Quotient rule you mean xD
u=x^2, v=ln(x)
u'=2x, v'=1/x
y'=(vu'-uv')/v^2 (chain rule)
=[2xln(x)-x]/(lnx)^2
=x[2ln(x)-1]/(lnx)^2
Question; Solve: tanx=3cotx
Quotient rule you mean xD
Dragonmaster262
Unorthodox top student
Re: 2 Unit Revising Marathon HSC '10
I'm having troubles reading your answer but I believe it is correct. Please post the next question.
I'm having troubles reading your answer but I believe it is correct. Please post the next question.
addikaye03
The A-Team
Re: 2 Unit Revising Marathon HSC '10
Also i posted a Q
ROFL! Yeah that's the one!Quotient rule you mean xD
Also i posted a Q
ninetypercent
ninety ninety ninety
Re: 2 Unit Revising Marathon HSC '10
tanx = 3cotx
tanx = 3/tanx
tan^2x = 3
tanx = +/- sqrt 3
x = pi(n) + pi/3
where n is an integer
Find the equation of the tangent(s) to x^2 + y^2 = 4, which are parallel to y= x + 3
tanx = 3cotx
tanx = 3/tanx
tan^2x = 3
tanx = +/- sqrt 3
x = pi(n) + pi/3
where n is an integer
Find the equation of the tangent(s) to x^2 + y^2 = 4, which are parallel to y= x + 3
Last edited by a moderator:
addikaye03
The A-Team
Re: 2 Unit Revising Marathon HSC '10
This Q can be solved geometrically. There is also an algebraic method. If not solved by a 2010 student by tomoz, i will show bothwhere n is an integer
Find the equation of the tangent(s) to x^2 + y^2 = 4, which are parallel to y= x + 3
Re: 2 Unit Revising Marathon HSC '10
All lines parallel to y=x+3 are of the form y=x+k, where k is a constant.
Thus if y=x+k is a tangent to x^2+y^2=4 the quadratic formed by subsituting y=x+k into x^2+y^2=4 will have a discriminant of zero.
Now sub y=x+kinto x^2+y^2=4
Thus we have x^2+(x+k)^2=4
x^2+x^2+2xk+k^2-4=0
2x^2+2xk+k^2-4=0
Δ=(2k)^2-4.2.(k^2-4)
=4k^2 - 8k^2 + 32
= -4k^2 + 32
But Δ=0
Thus 4k^2=32
k^2=16
k=+/- 4
Thus the required equation of tangent is y=x+4 or y=x-4
2U (ie. long) method:Find the equation of the tangent(s) to x^2 + y^2 = 4, which are parallel to y= x + 3
All lines parallel to y=x+3 are of the form y=x+k, where k is a constant.
Thus if y=x+k is a tangent to x^2+y^2=4 the quadratic formed by subsituting y=x+k into x^2+y^2=4 will have a discriminant of zero.
Now sub y=x+kinto x^2+y^2=4
Thus we have x^2+(x+k)^2=4
x^2+x^2+2xk+k^2-4=0
2x^2+2xk+k^2-4=0
Δ=(2k)^2-4.2.(k^2-4)
=4k^2 - 8k^2 + 32
= -4k^2 + 32
But Δ=0
Thus 4k^2=32
k^2=16
k=+/- 4
Thus the required equation of tangent is y=x+4 or y=x-4
- Joined
- Feb 16, 2005
- Messages
- 8,458
- Gender
- Male
- HSC
- 2006
Re: 2 Unit Revising Marathon HSC '10
If a(x) and b(x) are even functions while c(x) and d(x) are odd functions, prove that:
(i) a(x).b(x) is an even function
(ii) a(x).c(x) is an odd function
(iii) c(x).d(x) is an even function
If a(x) and b(x) are even functions while c(x) and d(x) are odd functions, prove that:
(i) a(x).b(x) is an even function
(ii) a(x).c(x) is an odd function
(iii) c(x).d(x) is an even function
Re: 2 Unit Revising Marathon HSC '10
If c(x) and d(x) are odd functions, c(-x)=-c(x) and d(-x)=-d(x)
(i) Let f(x)=a(x).b(x)
Thus f(-x)=a(-x).b(-x) = a(x).b(x) = f(x)
(ii) Let f(x) = a(x).c(x)
Thus f(-x)=a(-x).c(-x) = a(x).-c(x) = -a(x).c(x) = -f(x)
(iii) Let f(x)=c(x).d(x)
Thus f(-x)=c(-x).d(-x) = -c(x).-d(x) = c(x).d(x) = f(x)
Question: Solve for x: |x - 1| = -5
If a(x) and b(x) are even functions, a(-x)=a(x) and b(-x)=b(x)If a(x) and b(x) are even functions while c(x) and d(x) are odd functions, prove that:
(i) a(x).b(x) is an even function
(ii) a(x).c(x) is an odd function
(iii) c(x).d(x) is an even function
If c(x) and d(x) are odd functions, c(-x)=-c(x) and d(-x)=-d(x)
(i) Let f(x)=a(x).b(x)
Thus f(-x)=a(-x).b(-x) = a(x).b(x) = f(x)
(ii) Let f(x) = a(x).c(x)
Thus f(-x)=a(-x).c(-x) = a(x).-c(x) = -a(x).c(x) = -f(x)
(iii) Let f(x)=c(x).d(x)
Thus f(-x)=c(-x).d(-x) = -c(x).-d(x) = c(x).d(x) = f(x)
Question: Solve for x: |x - 1| = -5
Last edited:
violentdelights
Member
- Joined
- Jan 12, 2010
- Messages
- 808
- Gender
- Female
- HSC
- 2010
Re: 2 Unit Revising Marathon HSC '10
x = - 4 and 6
Find the eqn of the locus of the point so that it is equidistant from points 3, 2 and -1, 5
x = - 4 and 6
Find the eqn of the locus of the point so that it is equidistant from points 3, 2 and -1, 5
violentdelights
Member
- Joined
- Jan 12, 2010
- Messages
- 808
- Gender
- Female
- HSC
- 2010
Re: 2 Unit Revising Marathon HSC '10
Our teacher taught us that you must find
x - 1 = -5 normally without absolute values
and then find
-(x - 1) = -5
Hmm. How'd you do it?
Really? I'm not thinking well...Wrong.
Our teacher taught us that you must find
x - 1 = -5 normally without absolute values
and then find
-(x - 1) = -5
Hmm. How'd you do it?
ninetypercent
ninety ninety ninety
Re: 2 Unit Revising Marathon HSC '10
^ there is no solution
as -5 is negative
^ there is no solution
as -5 is negative
ninetypercent
ninety ninety ninety
Re: 2 Unit Revising Marathon HSC '10
^2 + (y-2)^2} = \sqrt{(x+1)^2 + (y-5)^2}\\ (x-3)^2 + (y-2)^2=(x+1)^2 + (y-5)^2\\ x^2 - 6x + 9 + y^2 - 4y + 4 = x^2 + 2x + 1 + y^2 - 10y + 25\\ 8x-6y+13 = 0)
Find the locus of the points that move equidistant from the line y = 3 and the point (3,4)
Find the eqn of the locus of the point so that it is equidistant from points 3, 2 and -1, 5
Find the locus of the points that move equidistant from the line y = 3 and the point (3,4)
