The region between the curve y=e^(-x^2), the x axis and the lines x=0 and x=N where N>0 is rotated about the y-axis to form a solid of revolution.
Use the method of cylindrical shells to find the volume of this solid in terms of N.
Now, when I do that, I get
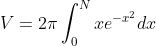
which is right. Now I use integration by parts and but in the solutions, it completely drops off the second part. Why is this?
Use the method of cylindrical shells to find the volume of this solid in terms of N.
Now, when I do that, I get
which is right. Now I use integration by parts and but in the solutions, it completely drops off the second part. Why is this?
