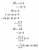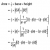vectors help pls (1 Viewer)

[sarbear.h]

theres sm questions idk how to do.. ill paste them below:

 

[Scrambled]

Heya I think I’ve got the first two at least but not too sure bout the last :/

 

[C2H6O]

I don’t have anywhere to work this out rn but for the third one maybe you’d have a circle with radius 4root5 centred at A, and C can be on the circle. Then use the side length of AB and AC and the area formula 1/2 a b sin C to find the angle BAC and where on the circle point C is (there should be 2) then use trig to find the 2 possible values of AC

 

[C2H6O]

I don’t have anywhere to work this out rn but for the third one maybe you’d have a circle with radius 4root5 centred at A, and C can be on the circle. Then use the side length of AB and AC and the area formula 1/2 a b sin C to find the angle BAC and where on the circle point C is (there should be 2) then use trig to find the 2 possible values of AC

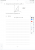
Actually I haven’t done any working there might be 4 total solutions, 1 acute angle, 1 obtuse angle, and then the same angles flipped iykwim

 

[=)(=]

theres sm questions idk how to do.. ill paste them below:
View attachment 47247View attachment 47248View attachment 47249

Are these from girra?

 

[sarbear.h]

Are these from girra?

nah chatties

 

[sarbear.h]

Actually I haven’t done any working there might be 4 total solutions, 1 acute angle, 1 obtuse angle, and then the same angles flipped iykwim

i might be cooked.. my exam is later today

 

[alphxreturns]

i might be cooked.. my exam is later today

do u have solutions for the 3rd one? so i dont embarass myself may be on the right track rn

 

[sarbear.h]

do u have solutions for the 3rd one? so i dont embarass myself may be on the right track rn

i dont ahaha.. i only need help on the third one now.. i got sm friends to show me q11
if it makes it better u can pm it to me?

 

[alphxreturns]

can't pm images





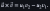
ok we use these, as well as the point distance formula (for 4√5)

so you get x^2 + y^2 = 80 (from point distance formula) ----- (1)

and ±10 = 3y-x --------(2)

2 cases with each form of (2)

which, when subbed into (1), gets a quadratic that yields another 2 solutions each (from the ± in the quadratic formula)

and boom you got 4 solutions just like C2H60 said


** not sure if this is the right approach but there ya go... i didn't know those identities at the top existed before this LOL forgot everything vectors already

 

[sarbear.h]

View attachment 47258

View attachment 47259

ok we use these, as well as the point distance formula (for 4√5)

so you get x^2 + y^2 = 80 (from point distance formula) ----- (1)

and ±10 = 3y-x --------(2)

2 cases with each form of (2)

which, when subbed into (1), gets a quadratic that yields another 2 solutions each (from the ± in the quadratic formula)

and boom you got 4 solutions just like C2H60 said


** not sure if this is the right approach but there ya go... i didn't know those identities at the top existed before this LOL forgot everything vectors already

is v1 being the x component and v2 the y component


(i meant like send a google drive link to ur pic lol)

 

[alphxreturns]

is v1 being the x component and v2 the y component

yeah AB being (3,1) and AC being (x,y)

 

[snodgrass1001]