asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
This was in our first asst...which I lost marks on. Anyway I was looking through the proof again and tried it again...Does it work?
Prove by induction
 \left(1+\frac{1}{2^3}\right) \left(1+\frac{1}{3^3}\right) \cdots \left(1+\frac{1}{n^3}\right) $ for $ n\geq1)
The solution gave

In the inductive step, they say
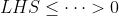
My question is...is that even proving the case when the LHS is in between? If you know what I mean... That is, by putting . I have imagined a number line like this.
. I have imagined a number line like this.

It doesn't account for the two cases...??? Only case 2 would prove the result is true, but with 1 you don't know exactly where LHS is
Thanks for any insights or solution.
NB THERE IS A TYPO (k+1)^2 instead of (k+1)^3 but it does not change the solution.
Prove by induction
The solution gave

In the inductive step, they say
My question is...is that even proving the case when the LHS is in between? If you know what I mean... That is, by putting

It doesn't account for the two cases...??? Only case 2 would prove the result is true, but with 1 you don't know exactly where LHS is
Thanks for any insights or solution.
NB THERE IS A TYPO (k+1)^2 instead of (k+1)^3 but it does not change the solution.
Attachments
-
48.1 KB Views: 51
Last edited:


