Could you add A(x) and B(x) to get 2x^3 + (a+b)x^2 - 2x + (a+b)
Then sub a+b = 0
A(x) + B(x) = 2x^3 - 2x = 2x(x^2 -1)
So the factor would be x^2 - 1 since if both A(x) and B(x) are divisible by the factor then their sum must also be divisible by the same factor.
Note that x=0 is not a factor as a cannot equal b which cannot equal 0.
This is a pretty neat idea! If we were being pedantic though, it hasn't been technically proven that A(x) and B(x) have a common factor. You've just shown that if there IS a common factor, it must be
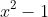
. Just because a term is a factor of the sum of two polynomials doesn't mean it is a factor of the original two polynomials. You still need to show that A(x) and B(x) actually have a common factor of degree 2.
A more standard way to do it would be to use the substitution a = -b in A(x) to get
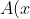 = x^3 + ax^2 - x - a)
. You can then try to factorise this by grouping the right terms to get
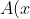 = x(x^2-1) + a(x^2 - 1) = (x+a)(x^2 - 1))
.
Similarly,
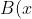 = (x-a)(x^2 - 1))
, and you can see that x^2 - 1 is a common factor. Since
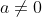
, they are not identical polynomials.

